Comments

• Must know \(p(s',r|s,a)\) to apply DP
• DP only applies to finite (and small) MDPs
• Have to approximate otherwise
• DP basis for understanding approximation methods
• DP learns \(v_\ast\) and \(q_\ast\), then distill \(\pi_\ast\)

Optimal Value Function Recursions

\[ \begin{align} v_\ast(s) &= \max_a E[R_{t+1} + \gamma v_\ast(S_{t+1}) | S_t=s,A_t=a] \\ &= \max_a \sum_{s',r} p(s',r|s,a) [r+\gamma v_\ast(s')] \\ q_\ast(s,a) &= E[R_{t+1}+\gamma \max_{a'} q_\ast(S_{t+1},a') | S_t=s,A_t=a] \\ &= \sum_{s',r} p(s',r|s,a) [r + \gamma \max_{a'}q_\ast(s',a')] \end{align} \]

Value Functions Recursions

\[ \begin{align} v_\pi(s) &= \sum_a \pi(a|s) \sum_{s',r} \left[ r + \gamma v_\pi(s') \right]p(s',r|s,a) \\ q_\pi(s,a) &= \sum_{s',r} p(s',r|s,a) \left[ r + \gamma \sum_{a'} \pi(s'|a') q_\pi(s',a') \right] \end{align} \]

Policy Evaluation (Prediction)

Policy evaluation (prediction) is computing \(v_\pi\) for policy \(\pi\)

Computing \(v_\pi\) for Policy \(\pi\)

Bellman’s equations (could solve as linear system):

\[ v_\pi(s) = \sum_a \pi(a|s) \sum_{s',r} p(s',r|s,a) [r+\gamma v_\pi(s')] \]

Iterative policy evaluation (expected update):

\[ v_{k+1}(s) = \sum_a \pi(a|s) \sum_{s',r} p(s',r|s,a) [r+\gamma v_k(s')] \]

\(v_k(s) \rightarrow v_\pi\)

In-place Computations

• Need two arrays to update all states in parallel, or
• Do in-place computations and update sequentially

Algorithm

Examples

• Revisiting grid world of example 3.5
• See example 4.1 on page 76 and the restults of iterative policy evaluation (prediction) on page 77

Exercise

• What does iterative policy evaluation (prediction) look like for \(q_\pi\)?
• Discuss storage requirements compared with \(v_\pi\).

Exercise Answer

\[ q_{k+1}(s,a) = \sum_{s',r} p(s',r|s,a) \left[ r + \gamma \sum_{a'} \pi(s'|a') q_k(s',a') \right] \]

• Storing \(v_\pi(s)\) requires \(|\mathcal{S}|\) locations
• Storing \(q_\pi(s,a)\) requires \(|\mathcal{S}| \times |\mathcal{A}|\) locations

Back to Gridworld

• Let’s go back to grid world and solve for \(q_\pi\). Click here

Policy Improvement

Go to notes.

Policy Iteration

\[ \pi_0 \overset{\text{E}}{\longrightarrow} v_{\pi_0} \overset{\text{I}}{\longrightarrow} \pi_1 \overset{\text{E}}{\longrightarrow} v_{\pi_1}\overset{\text{I}}{\longrightarrow} \cdots \overset{\text{I}}{\longrightarrow} \pi_\ast \overset{\text{E}}{\longrightarrow} v_\ast \]

Policy Iteration Algorithm

Policy Iteration Summary

• Policy iteration step 1: Policy evaluation (prediction) - iteratively sweep over states
• Policy iteration step 2: Policy improvement

Value Iteration Summary

• Value iteration step 1: Policy evaluation (prediction) - do just one sweep
• Value iteration step 2: Policy improvement

\[ v_{k+1} = \max_a \sum_{s',r} p(s',r|s,a) [r + \gamma v_k(s')] \]

• Combines improvement and evaluation in one eq.
• Iterated version of Bellman’s eq. for optimal value \(v_\ast\)

Value Iteration Algorithm

Family of Value Iteration Algs.

\[ \begin{alignat}{2} v_{k+1} &= \sum_a \pi(a|s)& &\sum_{s',r} p(s',r|s,a) [r + \gamma v_k(s')] \\ v_{k+1} &= \max_a & &\sum_{s',r} p(s',r|s,a) [r + \gamma v_k(s')] \end{alignat} \]

• Mix policy evaluation sweeps (1st eq.) with value iteration sweeps (2nd eq.)
• Expectation (1st eq.) and maximization (2nd eq.)

Homework

• Work the Gambler’s Problem in example 4.2 on page 84. Use value iteration.
• Do exercise 4.9
• Do exercise 4.10

Asynchronous DP

• In-place iterative DP algorithms not organized by linear sweeps over state space
• Update values in any order
• Update values in some states more often than in others (can’t ignore any state)
• Update in stochastic manner
• For convergence guarantee each state must be visited an infinite number of times
• Update based on what agent actually experiences

Various Approaches

• Policy Iteration
  • Make \(v_{k+1}\) consistent with \(\pi_k\) (policy evaluation)
  • Make \(\pi_{k+1}\) greedy wrt \(v_{k+1}\) (policy improvement)
• Value Iteration
  • Truncate policy evaluation (to one sweep)
  • Mixed numbers of evaluation and improvement steps (full sweeps)
• Asynchronous DP
  • Partial sweeps
  • Random sweeps

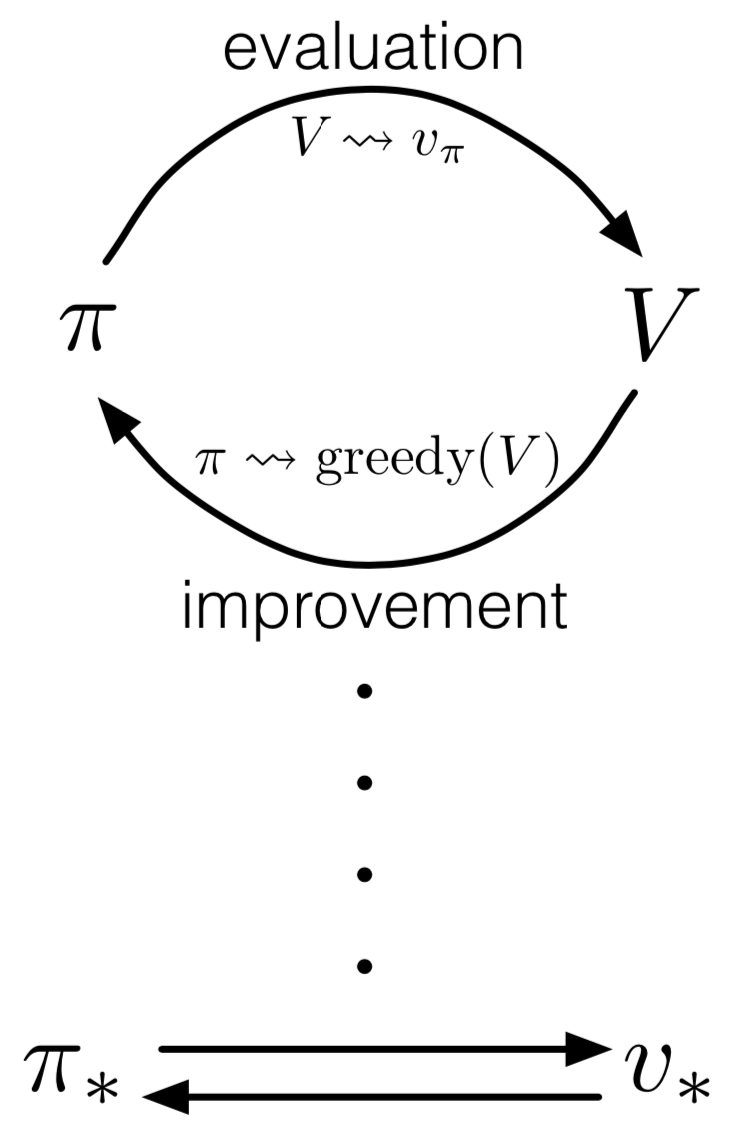
Generalized Policy Iteration

• Let policy evaluation and policy improvement processes interact
• “All” RL methods are GPI: have values and policies
  • Policies being improved wrt values
  • Values driving toward agreement with policy
• Evaluation and improvement processes compete

Generalized Policy Iteration

Solution Methods

• Exhaustive search is expensive or intractable
• Linear programming can efficiently solve MDPs but become impractical for smaller numbers of states
• DP is actually quite efficient (up to millions of states)
• DP convergence typically better than theoretical worst case
• Asynch. DP preferred because only a few states along optimal solution trajectories