Chapter 4: Dynamic Programming
Jake Gunther
2019/13/12
Background & Review
Optimal Value Function Recursions
\[ \begin{align} v_\ast(s) &= \max_a E[R_{t+1} + \gamma v_\ast(S_{t+1}) | S_t=s,A_t=a] \\ &= \max_a \sum_{s',r} p(s',r|s,a) [r+\gamma v_\ast(s')] \\ q_\ast(s,a) &= E[R_{t+1}+\gamma \max_{a'} q_\ast(S_{t+1},a') | S_t=s,A_t=a] \\ &= \sum_{s',r} p(s',r|s,a) [r + \gamma \max_{a'}q_\ast(s',a')] \end{align} \]
Value Functions Recursions
\[ \begin{align} v_\pi(s) &= \sum_a \pi(a|s) \sum_{s',r} \left[ r + \gamma v_\pi(s') \right]p(s',r|s,a) \\ q_\pi(s,a) &= \sum_{s',r} p(s',r|s,a) \left[ r + \gamma \sum_{a'} \pi(s'|a') q_\pi(s',a') \right] \end{align} \]
Policy Evaluation (Prediction)
Policy Evaluation (Prediction)
Policy evaluation (prediction) is computing \(v_\pi\) for policy \(\pi\)
Computing \(v_\pi\) for Policy \(\pi\)
Bellman’s equations (could solve as linear system):
\[ v_\pi(s) = \sum_a \pi(a|s) \sum_{s',r} p(s',r|s,a) [r+\gamma v_\pi(s')] \]
Iterative policy evaluation (expected update):
\[ v_{k+1}(s) = \sum_a \pi(a|s) \sum_{s',r} p(s',r|s,a) [r+\gamma v_k(s')] \]
\(v_k(s) \rightarrow v_\pi\)
In-place Computations
- Need two arrays to update all states in parallel, or
- Do in-place computations and update sequentially
Algorithm

Examples
- Revisiting grid world of example 3.5
- See example 4.1 on page 76 and the restults of iterative policy evaluation (prediction) on page 77
Exercise
- What does iterative policy evaluation (prediction) look like for \(q_\pi\)?
- Discuss storage requirements compared with \(v_\pi\).
Exercise Answer
\[ q_{k+1}(s,a) = \sum_{s',r} p(s',r|s,a) \left[ r + \gamma \sum_{a'} \pi(s'|a') q_k(s',a') \right] \]
- Storing \(v_\pi(s)\) requires \(|\mathcal{S}|\) locations
- Storing \(q_\pi(s,a)\) requires \(|\mathcal{S}| \times |\mathcal{A}|\) locations
Back to Gridworld
- Let’s go back to grid world and solve for \(q_\pi\). Click here
Policy Improvement
Policy Improvement
Policy Iteration
Policy Iteration
\[ \pi_0 \overset{\text{E}}{\longrightarrow} v_{\pi_0} \overset{\text{I}}{\longrightarrow} \pi_1 \overset{\text{E}}{\longrightarrow} v_{\pi_1}\overset{\text{I}}{\longrightarrow} \cdots \overset{\text{I}}{\longrightarrow} \pi_\ast \overset{\text{E}}{\longrightarrow} v_\ast \]
Policy Iteration Algorithm

Value Iteration
Policy Iteration Summary
- Policy iteration step 1: Policy evaluation (prediction) - iteratively sweep over states
- Policy iteration step 2: Policy improvement
Value Iteration Summary
- Value iteration step 1: Policy evaluation (prediction) - do just one sweep
- Value iteration step 2: Policy improvement
\[ v_{k+1} = \max_a \sum_{s',r} p(s',r|s,a) [r + \gamma v_k(s')] \]
- Combines improvement and evaluation in one eq.
- Iterated version of Bellman’s eq. for optimal value \(v_\ast\)
Value Iteration Algorithm

Family of Value Iteration Algs.
\[ \begin{alignat}{2} v_{k+1} &= \sum_a \pi(a|s)& &\sum_{s',r} p(s',r|s,a) [r + \gamma v_k(s')] \\ v_{k+1} &= \max_a & &\sum_{s',r} p(s',r|s,a) [r + \gamma v_k(s')] \end{alignat} \]
- Mix policy evaluation sweeps (1st eq.) with value iteration sweeps (2nd eq.)
- Expectation (1st eq.) and maximization (2nd eq.)
Homework
- Work the Gambler’s Problem in example 4.2 on page 84. Use value iteration.
- Do exercise 4.9
- Do exercise 4.10
Asynchronous Dynamic Programming
Asynchronous DP
- In-place iterative DP algorithms not organized by linear sweeps over state space
- Update values in any order
- Update values in some states more often than in others (can’t ignore any state)
- Update in stochastic manner
- For convergence guarantee each state must be visited an infinite number of times
- Update based on what agent actually experiences
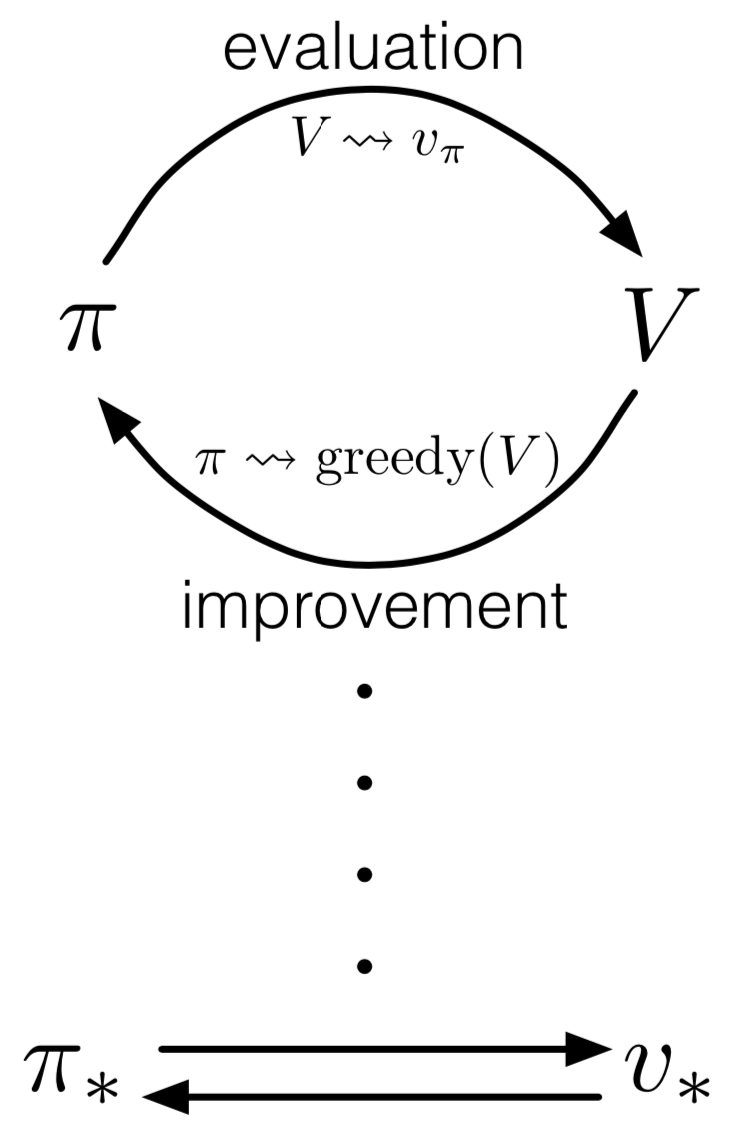
Generalized Policy Iteration
Various Approaches
- Policy Iteration
- Make \(v_{k+1}\) consistent with \(\pi_k\) (policy evaluation)
- Make \(\pi_{k+1}\) greedy wrt \(v_{k+1}\) (policy improvement)
- Value Iteration
- Truncate policy evaluation (to one sweep)
- Mixed numbers of evaluation and improvement steps (full sweeps)
- Asynchronous DP
- Partial sweeps
- Random sweeps
Generalized Policy Iteration
- Let policy evaluation and policy improvement processes interact
- “All” RL methods are GPI: have values and policies
- Policies being improved wrt values
- Values driving toward agreement with policy
- Evaluation and improvement processes compete
Generalized Policy Iteration
Solution Methods
Solution Methods
- Exhaustive search is expensive or intractable
- Linear programming can efficiently solve MDPs but become impractical for smaller numbers of states
- DP is actually quite efficient (up to millions of states)
- DP convergence typically better than theoretical worst case
- Asynch. DP preferred because only a few states along optimal solution trajectories
Comments