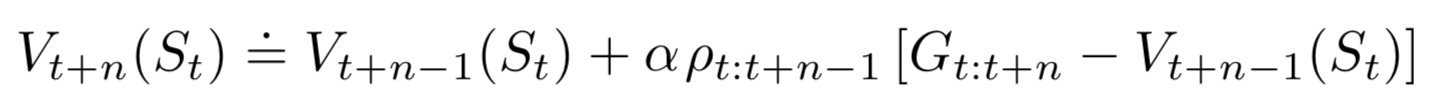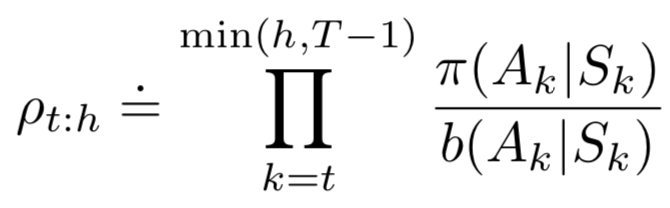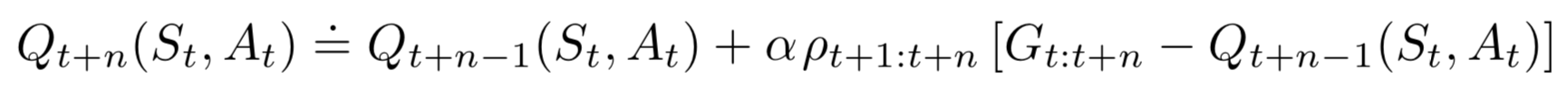Chapter 7: \(n\)-step Bootstrapping
Jake Gunther
2020/15/1
\(n\)-step Bootstrapping
Background
- Unify Monte Carlo (MC) methods and the one-step temporal-difference (TD) methods
- “… shift from one to the other smoothly as needed …”
- “… span the spectrum with MC methods at one end and one-step TD methods at the other.”
- “… free you from the tyranny of the time step.”
MC & TD Review
- MC: Update \(V(S)\) based on entire sequence of rewards until end of episode (observed value of \(G\))
- TD: Update \(V(S)\) using \(R + \gamma V(S')\) as proxy for return \(G\)
- What kind of update lies between these extremes?
- Update \(V(S)\) based on number of rewards (more than one but less than all till termination)
\(n\)-step TD Prediction
\(n\)-step TD Prediction
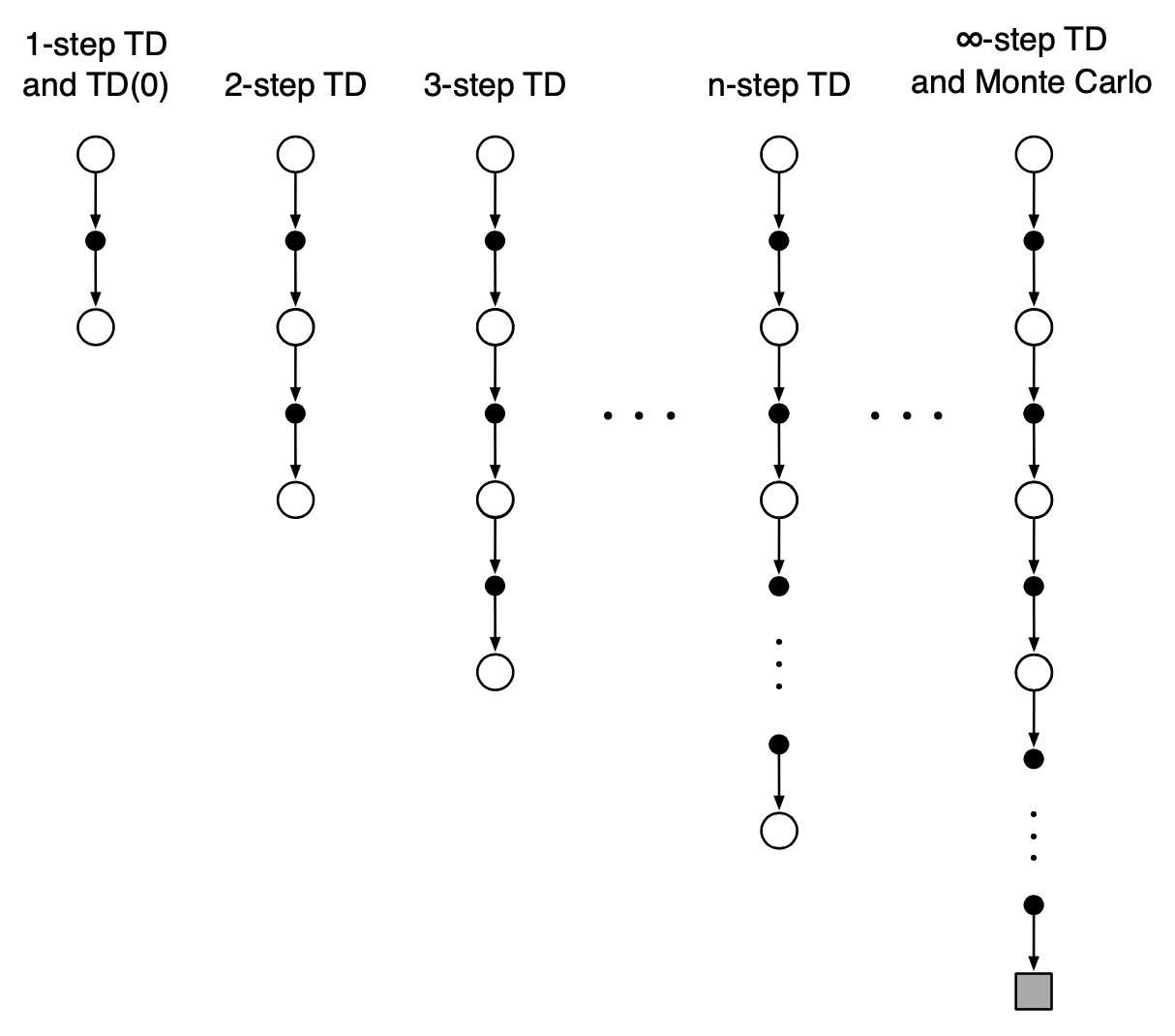
Monte Carlo Target
\[ \begin{align} G_t &= R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots + \gamma^{T-t-1} R_{T} \\ V(S_t) &= V(S_t) + \alpha [G_t - V(S_t)] \end{align} \]
One-Step TD target
\[ \begin{align} G_{t:t+1} &= R_{t+1} + \gamma V(S_{t+1}) \\ V(S_t) &= V(S_t) + \alpha [G_{t:t+1} - V(S_t)] \end{align} \]
\(V(S_{t+1})\) used as a surrogate for returns following \(S_{t+1}\)
Two-Step TD target
\[ \begin{align} G_{t:t+2} &= R_{t+1} + \gamma R_{t+2} + \gamma^2 V(S_{t+2}) \\ V(S_t) &= V(S_t) + \alpha [G_{t:t+2} - V(S_t)] \end{align} \]
\(V(S_{t+2})\) used as a surrogate for returns following \(S_{t+2}\)
\(n\)-Step TD target
\[ \begin{align} G_{t:t+n} &= R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^{n} V(S_{t+n}) \\ V(S_t) &= V(S_t) + \alpha [G_{t:t+n} - V(S_t)] \end{align} \]
\(V(S_{t+n})\) used as a surrogate for returns following \(S_{t+n}\)
Algorithm

Error Reduction Property
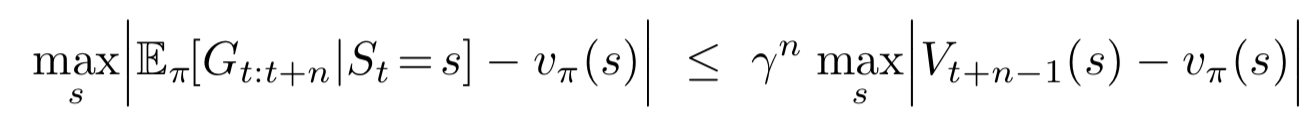
Guarantees that \(n\)-step TD methods converge to \(v_\pi\)
One-step TD and MC methods are special cases
Performance of \(n\)-step TD
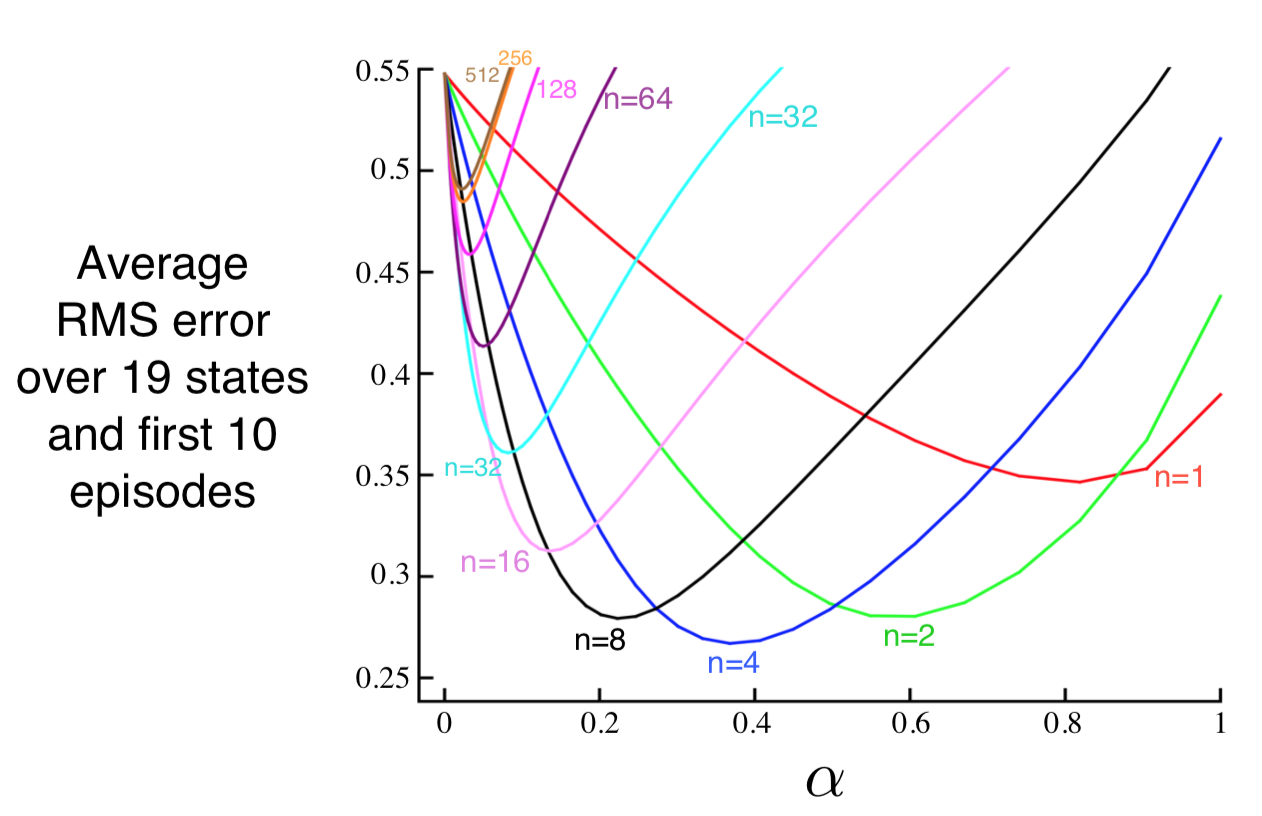
\(n\)-step SARSA
\(n\)-step SARSA
- Switch state \((s)\) for state-action pair \((s,a)\)
- Iteration for \(Q\)
- Use \(\varepsilon\)-greedy policy
\(n\)-step SARSA
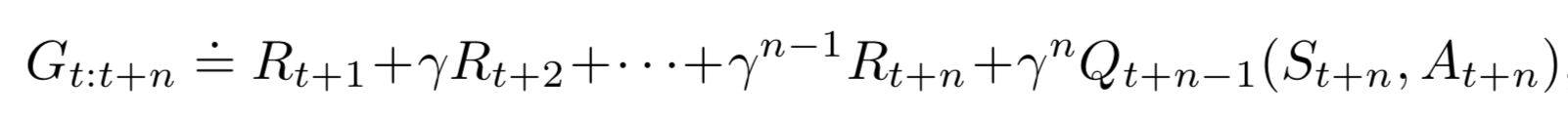
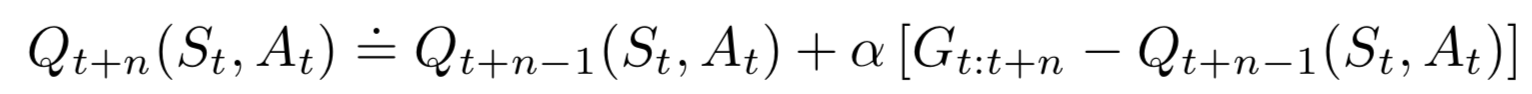

\(n\)-step SARSA learns more than 1-step SARSA
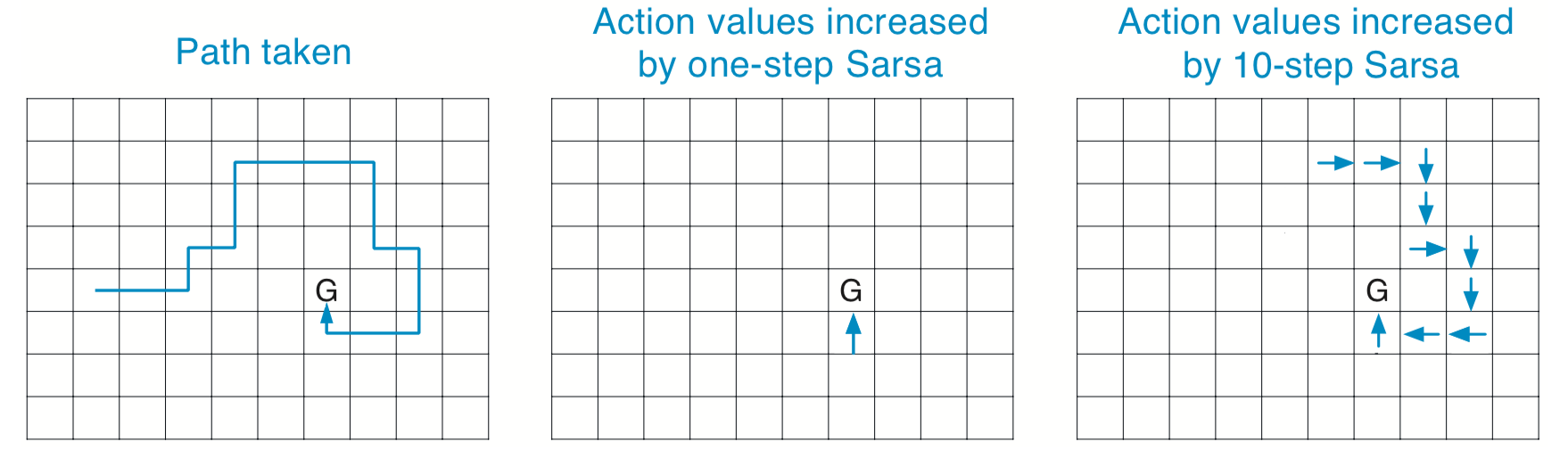
1-step strengthens only last action, \(n\)-step strengthens last \(n\) actions
more is learned from each episode
\(n\)-step Off-Policy TD
\(n\)-step Off-Policy TD