Chapter 3: Finite Markov Decision Processes
Jake Gunther
2019/13/12
Markov Decision Processes
Overview of MDPs
- Evaluative feedback
- Associative aspects
- Sequential decision making
- Tradeoff immediate vs. delayed rewards
- Bandits: \(q_\ast(a)\)
- MDPs: \(q_\ast(s,a)\) and \(v_\ast(s)\)
Agent-Environment Interface
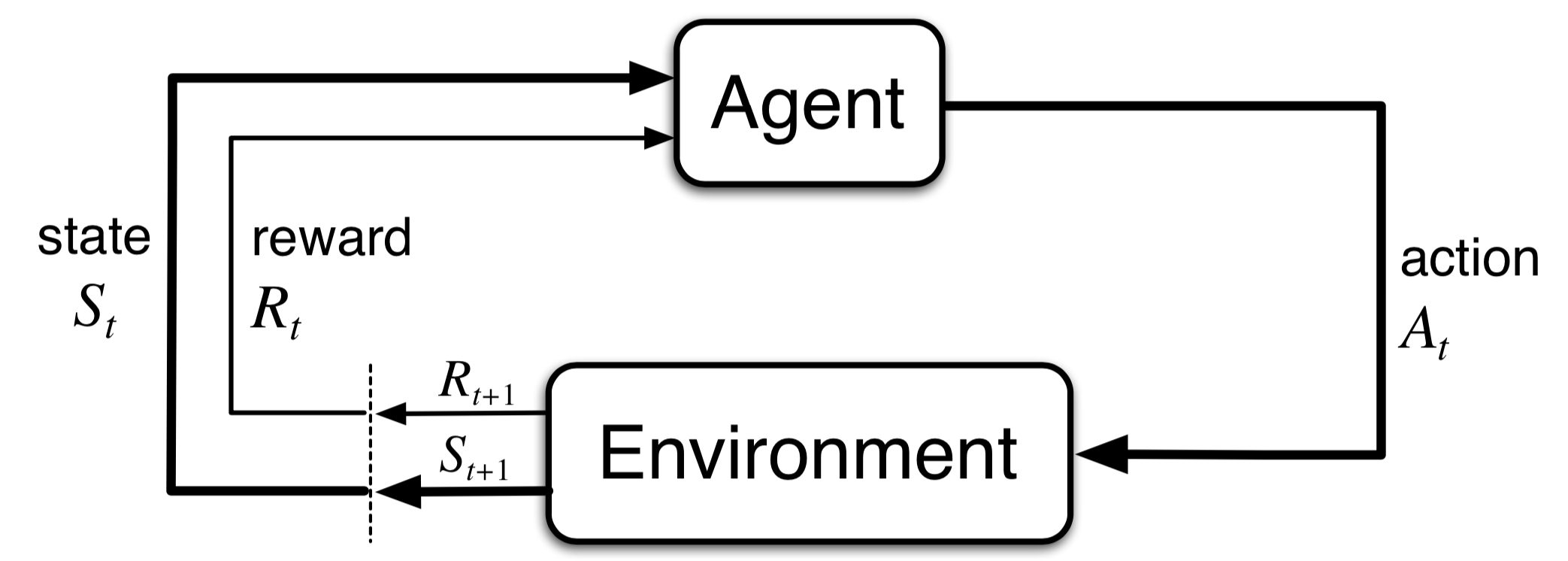
Problem Representation

“Any problem of learning goal-directed behavior can be reduced to three signals passing back and forth between an agent and its environment.”
- Choices (actions of agent)
- Basis for choices (states of environment)
- Goal definition (rewards to agent)
Agent-Environment Interface
- Interaction at discrete time steps, \(t=0, 1, 2, 3, \cdots\)
- Agent: chooses actions \(A_t \in \mathcal{A}(s)\)
- Environment: has a state \(S_t\in \mathcal{S}\)
- Environment: generates rewards \(R_t \in \mathcal{R}\)
- Trajectory: \(S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, R_3, S_3, \cdots\)
Time Steps
- \(t=0, 1, 2, 3, \cdots\)
- May refer to fixed intervals of real time
- May refer to arbitrary successive stages of decision making and acting
Actions
- \(A_t \in \mathcal{A}(s)\)
- Any decision we want to learn how to make
- Low-level controls - voltage on a motor (continuous)
- High-level decisions - have lunch (binary), go to graduate school (binary)
- Can be mental or computational (think about \(X\), focus on \(Y\))
States
- \(S_t\in \mathcal{S}\)
- Anything we can know that might be useful in decision making
- Low-level sensations (sensor readings)
- High-level and abstract (symbolic description of objects in a room)
- May include memory
- May be mental (not knowing: where are my keys)
- May be subjective (surprise in a clearly defined sense)
Rewards
- \(R_t \in \mathcal{R}\)
- Formalizes the goal of the agent
- Part of the environment
- Computed/derived inside natural or artificial (robotic) agents, but considered external to agent
Agent-Environment Boundary
- Environment: anything that cannot be changed arbitrarily by agent
- Boundary: limit of agent’s absolute control (but not of its knowledge)
- Robots: motors, linkages, sensors \(\in\) environment
- Person/animal: muscles, skeleton, sensory organs \(\in\) environment
Example: Bioreactor
- Objective: Determine temperature and stirring rate for bioreactor
- State: thermocouple, other sensors, ingredients, target chemicals
- Actions: target temperature and stirring rate (passed to lower level controller)
- Reward: rate of target chemical production
- States & actions: vectors
- Reward: scalar value
Example: Pick-and-Place Robot
- Objective: Control motion of robotic arm in repetitive task (fast smooth motion)
- State: Positions and velocities of linkages
- Action: Motor voltages
- Reward: +1 (for each pick-and-place success) - jerkiness of motion
Discuss these Examples
- Stop smoking
- Play Packman
- Invest wisely
- Driving to a destination (move the boundry around)
Look at Example 3.3
- Action set that depends on the state
- Markovity of states defined in graph
- Dynamics are tabulated (finite MDP)
Mathematical Formulation
Finite MDP
- \(\mathcal{S, A, R}\) are finite sets
- RVs \(S_t, A_t, R_t\) have PMFs
- MDP dynamics:
\[ \begin{gather} p(s',r | s, a) = \text{Pr}\left\{\begin{array}{c}S_t=s' \\ R_t=r\end{array} \bigg|\begin{array}{c} S_{t-1}=s \\ A_{t-1}=a\end{array}\right\} \\[1em] \sum_{s' \in \mathcal{S}} \sum_{r \in \mathcal{R}} p(s',r|s,a) = 1, \;\;\forall \;\; s\in \mathcal{S}, a\in \mathcal{A}(s) \end{gather} \]
Markov Property
- Not restriction on MDP
- Markovity is in the state
\[ (S_t,A_t) \mapsto S_{t+1} \]
Goals and Rewards
Goals
- Maximize total amount of reward received
- Don’t focus on immediate (short run) reward
- Focus on cumulative reward in the long run
Rewards
- Incentivize what you want the agent to learn
- If you want the agent to learn “to do something for us, then provide rewards to it in such a way that in maximizing them the agent will also achieve our goals.”
- Rewards communicate what to achieve, not how to achieve it
Chess
- Reward winning (what)
- Don’t reward subgoals (how)
- Taking opponent’s pieces (how)
- Controlling center of board (how)
- +10 for win (reward winning the game)
- -1 for each turn (reward winning the game in few moves)
Examples
Do these reward the right thing?
- Robotic walking - make reward proportional to forward motion on each time step
- Escape maze - reward is -1 for every time step
Returns and Episodes
Returns
- Choose \(A_t\) to maximize return \(G_t\)
- Return \(G_t\) is cumulative reward received after time \(t\)
- Return \(G_t = R_{t+1} + R_{t+2} + R_{t+3} + \cdots + R_T\)
- Return could be some other function of reward sequence
- Note: Action \(A_t\) cannot maximize \(G_{t-k}\) for \(k>0\)
Episodes
- Episode is a repeated interaction
- Starting state is known or drawn from distribution
- Ending in terminal state \(s\in \mathcal{S}^+\) at time \(T<\infty\)
- \(T\) is an RV
- Episodic tasks (games, mazes, etc.)
- Nonepisodic tasks continue without end
- Process control task
- Robot with long life span
- \(T=\infty\)
Discounting
Choose \(A_t\) to maximize discounted return \(G_t = \sum_{k=0}^\infty \gamma^k R_{t+k+1}\)
\(\gamma \in [0,1]\) is the discount rate
Discounting puts diminishing weight on future rewards
\(\gamma=0\) (myopic agent) focuses attention on immediate reward \(R_{t+1}\)
\(\gamma \rightarrow 1\) (farsighted agent)
Recursion
\[ \begin{align} G_t &= \sum_{k=0}^\infty \gamma^k R_{t+k+1} = R_{t+1} + \gamma G_{t+1} \quad \forall \quad t<T \\ G_t &= \sum_{k=0}^\infty \gamma^k = \frac{1}{1-\gamma}, \quad R_t = 1 \quad \forall \quad t \end{align} \]
Example: Cart-Pole
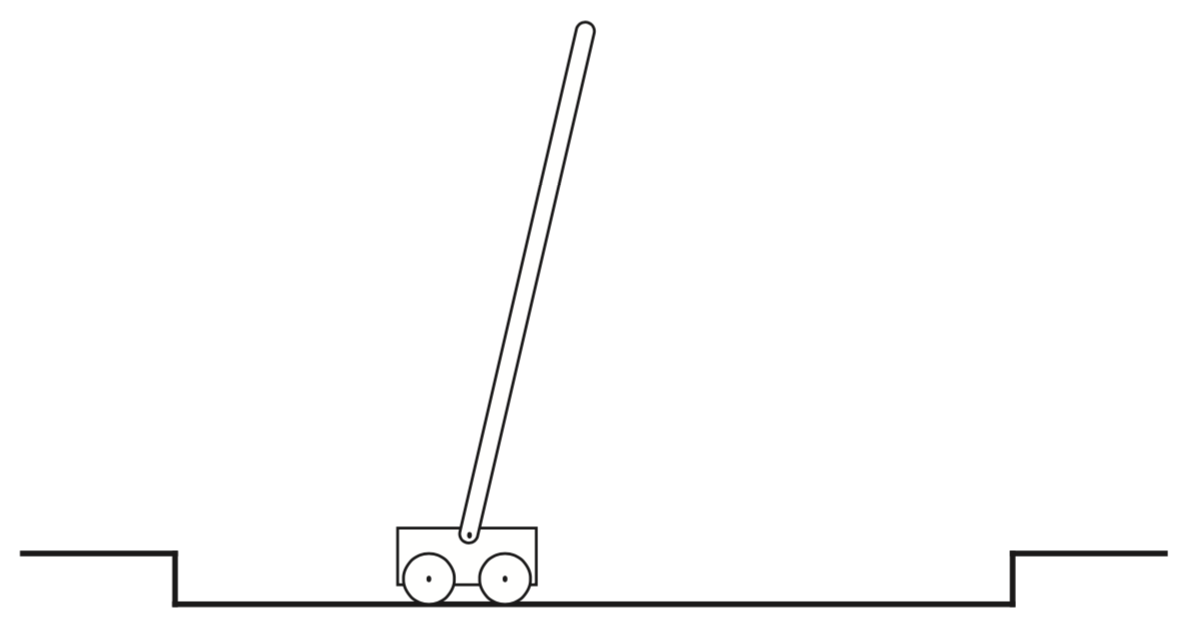
- Objective: Balance the pole and stay on track
- Initialize: Start with pole balanced in track center
- Episodic: \(R_t = +1\) when not fail (\(\gamma=1\))
- Q: What is \(G_t\)?
- A: The number of steps until failure
- This keeps pole balanced as long as possible (\(G_t\rightarrow\infty\))
Example: Cart-Pole

- Objective: Balance the pole and stay on track
- Initialize: Start with pole balanced in track center
- Continuing: \(R_t = -1\) for failure and \(R_t=0\) otherwise (with \(\gamma<1\))
- Return: \(G_t = -\gamma^K\) where \(K\) is the number of steps to failure
- This keeps pole balanced as long as possible

- Objective: Balance the pole and stay on track
- Initialize: Start with pole balanced in track center
- Episodic: \(R_t = -1\) for failure and \(R_t=0\) otherwise (with \(\gamma<1\))
- Return: \(G_t = -\gamma^{T-t-1}\)
Maze escape robot
- \(R_t=1\) for esacpe and \(R_t=0\) otherwise. Why doesn’t this work?
- How can we communicate through the reward what we want the robot to do?
Unified Notation
Task Types
- Episodic: \(S_{t,i}, A_{t,i}, R_{t,i}, \pi_{t,i}, T_i\) for the \(i^\text{th}\) episode
- Convention: Drop the \(i\) most of the time
- Continuing: \(S_{t}, A_{t}, R_{t}, \pi_{t}, T\)
- Same notation for both task types
Return
- Epsiodic: \(G_t = R_{t+1} + R_{t+2} + \cdots + R_{T}\)
- Continuing: \(G_t = R_{t+1} + R_{t+2} + R_{t+3} + \cdots\)
- Want same notation for both task types
- To unify notation, define absorbing (square) state for episodic task where rewards are zero

Unified Notation
\[ G_t = \sum_{k=0}^{T-t-1} \gamma^k R_{t+k+1} = \sum_{k=t+1}^T \gamma^{k-t-1} R_k \]
- Continuing: \(T=\infty\) and \(\gamma \in [0,1)\) (need convergence)
- Episodic: \(T<\infty\) and \(\gamma \in [0,1]\) (convergence guaranteed)
- Episode numbers not needed
Policies
Policy
\[ \begin{gather} \pi(a|s) = \text{Pr}\{A_t = a | S_t=s\} \\ a \in \mathcal{A}(s), \quad s \in \mathcal{S} \end{gather} \]
- Policy: How the agent chooses actions in the context of a state
- RL methods: How \(\pi\) changes based on experience
Value Functions
State-Value Function for Policy \(\pi\)
\[ v_\pi(s) = E_\pi[G_t | S_t=s] = E_\pi \left[\sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \bigg| S_t=s\right] \]
- Expected return (value) when starting in state \(s\) and following policy \(\pi\) thereafter
Action-Value for Policy \(\pi\)
\[ \begin{align} q_\pi(s,a) &= E_\pi[G_t | S_t=s, A_t=a] \\ &= E_\pi\left[\sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \bigg| S_t=s, A_t=a\right] \end{align} \]
- Expected return (value) of taking action \(a\) in state \(s\) and following policy \(\pi\) thereafter
Look Ahead (Monte Carlo Methods)
- Expectations in \(v_\pi\) and \(q_\pi\) can be estimated from sample averages over many episodes
- How? For each state maintain average return that followed that state under policy \(\pi\). This converges to \(v_\pi\).
- How? For each state-action pair maintain average return that followed under policy \(\pi\). This converges to \(q_\pi\).
Look Ahead (Approximation Methods)
- If too many states, then keeping averages in each state is not practical.
- Approximate \(v_\pi, q_\pi\) as parameterized functions (e.g. DNN) and adjust parameters to match observed returns.
Value Recursions
Exercises
- Give an equation for \(v_\pi\) in terms of \(q_\pi\) and \(\pi\) (solution)
- Given an equation for \(q_\pi\) in terms of \(v_\pi\) and four-argument \(p\) (solution)
Answers
\[ \begin{align} v_\pi(s) &= \sum_a q_\pi(s,a) \pi (s|a)\\ q_\pi(s,a) &= \sum_{s'} \sum_r \left[ r + \gamma v_\pi(s') \right]p(s',r|s,a) \end{align} \]
Backup Diagram for \(v_\pi\)
\[ v_\pi(s) = \sum_a q_\pi(s,a) \pi (s|a) \]
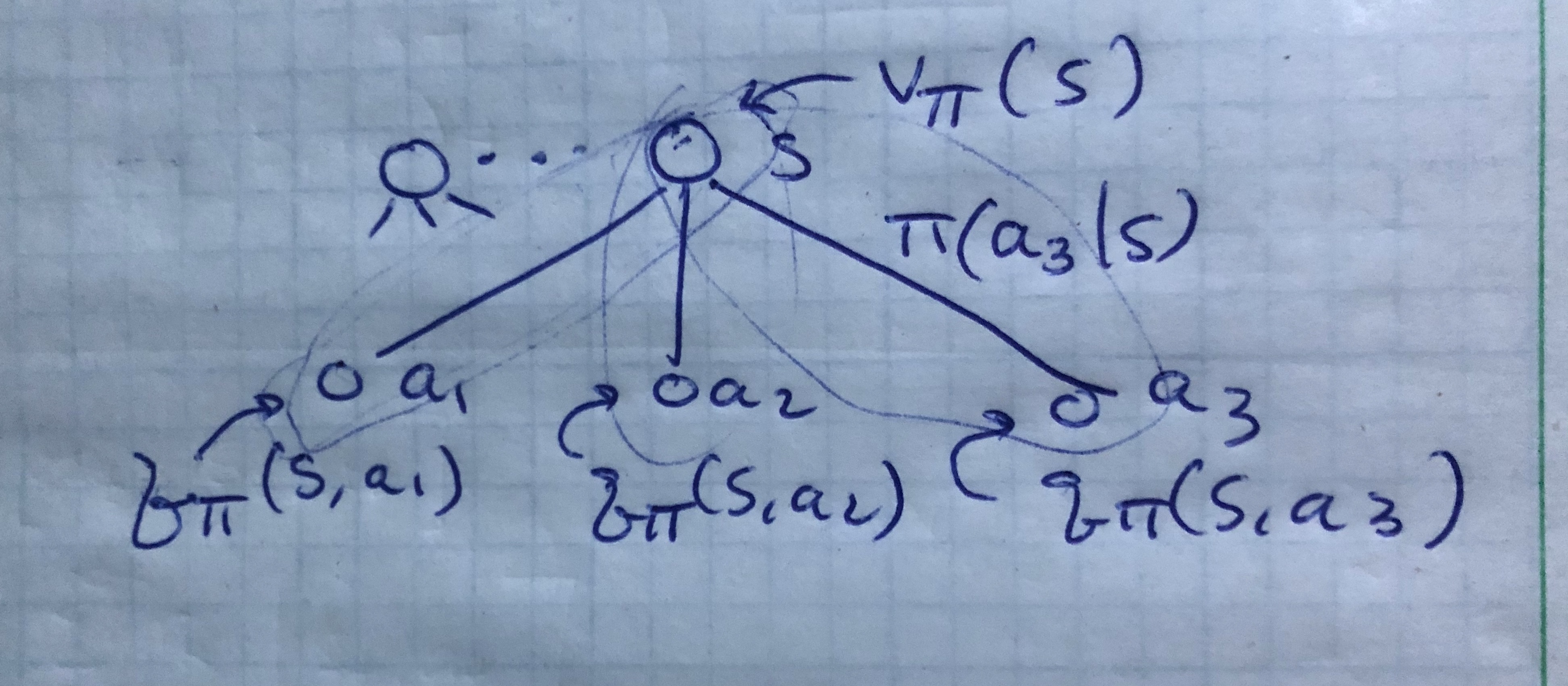
Backup Diagram for \(q_\pi\)
\[ q_\pi(s,a) = \sum_{s'} \sum_r \left[ r + \gamma v_\pi(s') \right]p(s',r|s,a) \]
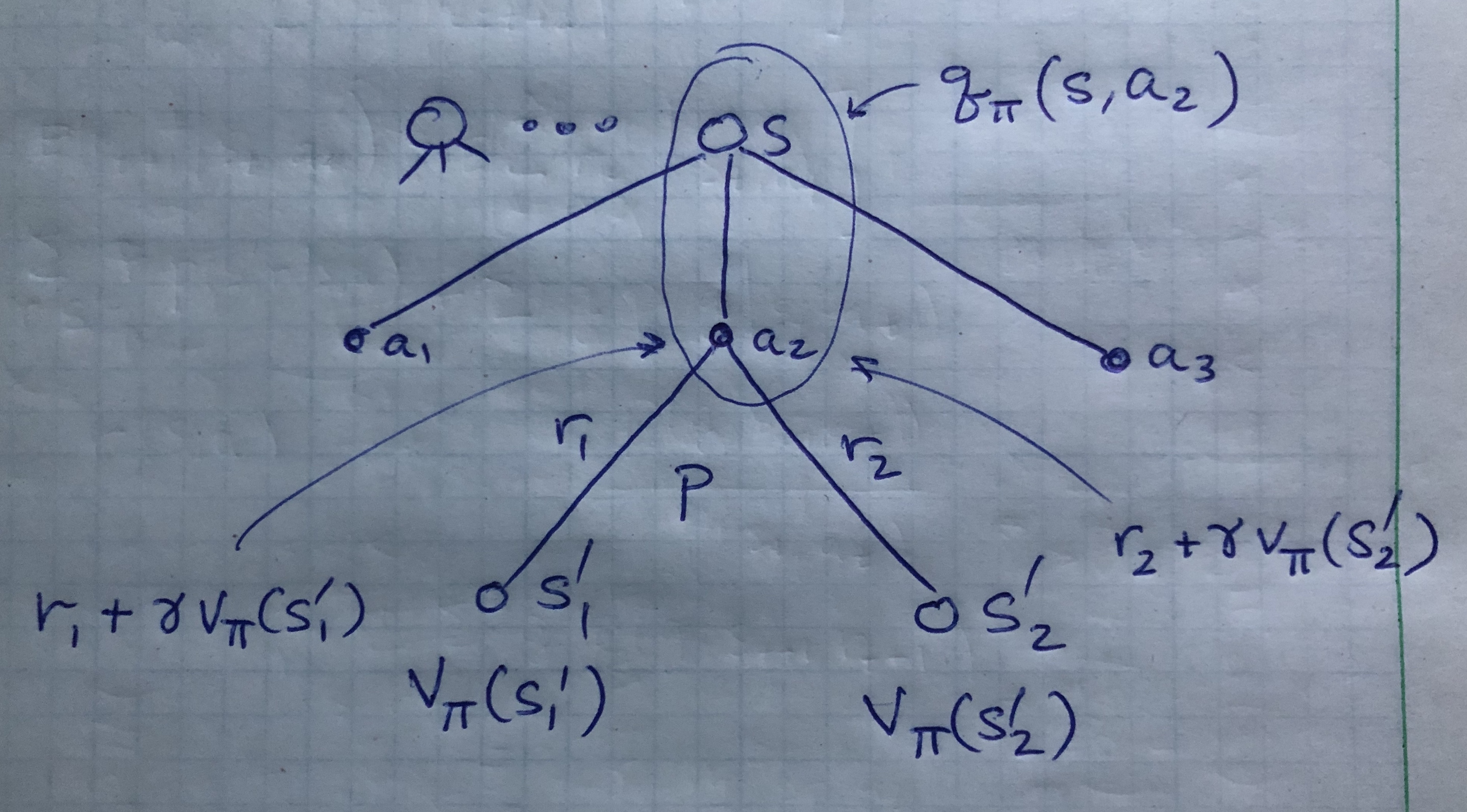
Value Recursion
Substitute \(v_\pi\)-\(q_\pi\) relations into one another to obtain recursions.
\[ \begin{align} v_\pi(s) &= \sum_a \pi(a|s) \sum_{s',r} \left[ r + \gamma v_\pi(s') \right]p(s',r|s,a) \\ q_\pi(s,a) &= \sum_{s',r} \left[ r + \gamma \sum_{a'} q_\pi(s',a') \pi(s'|a') \right]p(s',r|s,a) \end{align} \]
State-Value Recursion
\[ v_\pi(s) = \sum_a \pi(a|s) \sum_{s',r} \left[ r + \gamma v_\pi(s') \right]p(s',r|s,a) \]
- Consistency condition between \(v_\pi(s)\) and \(v_\pi(s')\)
- Expected value of \(r+\gamma v_\pi(s')\) over \(p(s',r,a|s) = \pi(a|s)p(s',r|s,a)\)
- Bellman equation for \(v_\pi\)
- \(v_\pi\) is unique solution to Bellman equation
- Bellman equation: Compute, approximate, learn \(v_\pi\)
Backup Diagram for \(v_\pi\)
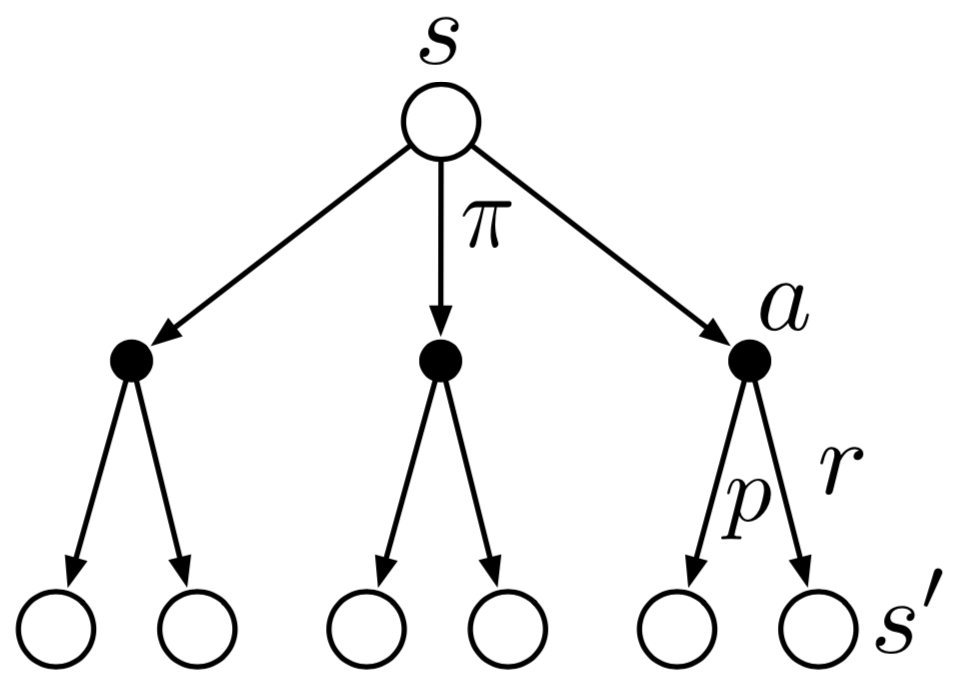
Graphical representation of \(v_\pi\) recursion from \(s'\) to \(s\)
- Start state \(s\) at top (open circle)
- Policy \(\pi\) gives action \(a\) (solid circle)
- Environment responds with reward \(r\) and next state \(s'\) according to probability \(p\)
Examples
Gridworld
- See Example 3.5 in text (page 60).
- Here are my calculations.
Optimality
Optimal Policies
- Value function defines a partial order for policies
\[ \pi \geq \pi' \quad \Leftrightarrow \quad v_\pi(s) \geq v_{\pi'}(s) \;\;\forall\;\;s \in \mathcal{S} \]
- An optimal policy exists but may not be unique
- Denote optimal policies by \(\pi_\ast\)
- Denote optimal state-value function \(v_\ast = v_{\pi_\ast}\)
Optimal Policies
\[ \begin{align} v_\ast(s) &= \max_\pi v_\pi(s) \;\;\forall\;\;s\in\mathcal{S} \\ q_\ast(s,a) &= \max_\pi q_\pi(s,a) \;\;\forall\;\;s\in\mathcal{S} \;\;\text{and}\;\; a\in\mathcal{A}(s) \end{align} \]
- The same policy optimizes both value functions
Relations
- Q: What does the optimal policy \(\pi_\ast\) look like?
- A: It puts all its weight on the best action (greed)
\[ \begin{gather} \pi_\ast(a|s) = \mathbb{1}_{a=a_\ast} = \begin{cases} 1, & a=a_\ast \\ 0, & \text{otherwise} \end{cases} \\[1em] v_\ast(s) = \sum_{a\in\mathcal{A}(s)} \pi_\ast(a|s) q_\ast(s,a) = \max_{a\in\mathcal{A}(s)} q_\ast(s,a) \end{gather} \]
Recursion for Optimal Value Function
Leveraging this derivation and \(\pi=\pi_\ast\), we have
\[ \begin{align} v_\ast(s) &= \max_a q_\ast(s,a) \\ &= \max_a E[R_{t+1} + \gamma G_{t+1} | S_t=s,A_t=a] \\ &= \max_a E[R_{t+1} + \gamma v_\ast(S_{t+1}) | S_t=s, A_t=a] \\ &= \max_a \sum_{s',r} p(s',r|s,a) [r + \gamma v_\ast(s')] \end{align} \]
Apply Greed
\[ \begin{align} v_\pi(s) &= \sum_a \pi(a|s) \sum_{s',r} \left[ r + \gamma v_\pi(s') \right]p(s',r|s,a) \\ v_\ast(s) &= \max_a \sum_{s',r} \left[ r + \gamma v_\ast(s') \right]p(s',r|s,a) \end{align} \]
\[ \sum_a \pi_\ast(a|s) \quad \overset{\text{greed}}{\longrightarrow} \quad \max_a \]
Recursion for Optimal Action-Value Function
Applying greed, we have
\[ \begin{align} q_\pi(s,a) &= \sum_{s',r} p(s',r|s,a) \left[ r + \gamma \sum_{a'} \pi(s'|a') q_\pi(s',a') \right] \\ q_\ast(s,a) &= \sum_{s',r} p(s',r|s,a)\left[ r + \gamma \max_{a'} q_\ast(s',a') \right] \end{align} \]
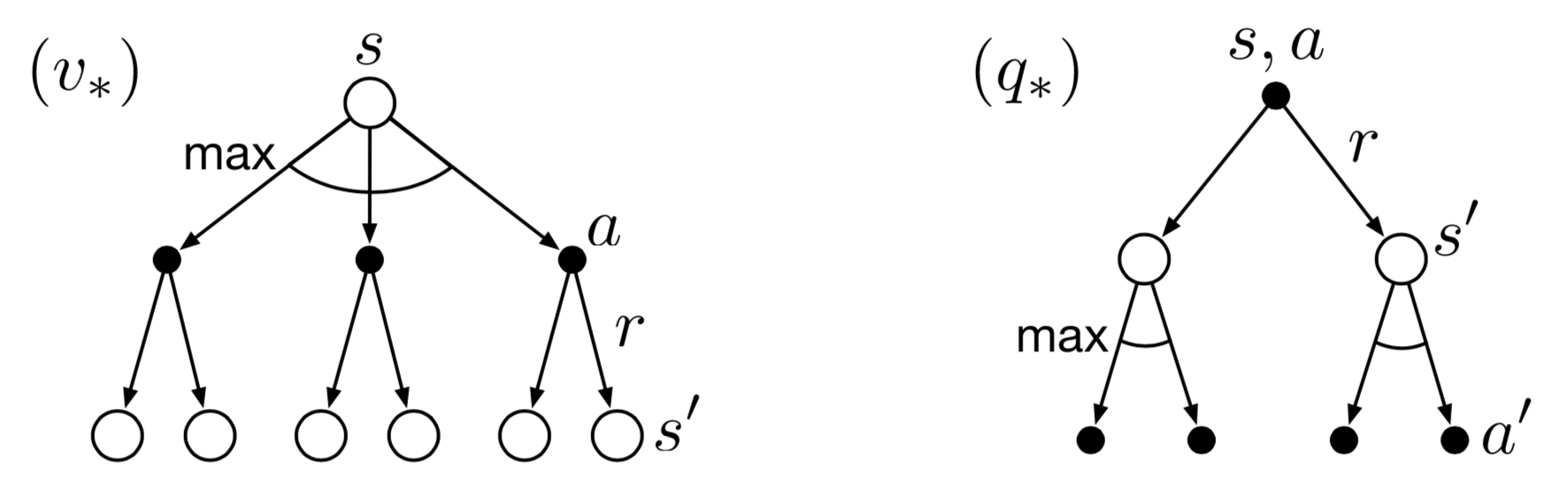
Backup Diagrams for Optimal Value Functions
Optimal Policy for Gridworld

(We don’t yet know how to find \(v_\ast\). Take this as given for now.)
Optimal Policy \(\leftarrow\) Optimal Value
- Given \(v_\ast(s)\), \(\pi_\ast(a|s)\) assigns non-zero probability to best action(s) and zero probability to all other actions
- Optimal policy \(\pi_\ast\) is greedy wrt optimal value \(v_\ast\)
- A one-step (short-run) search is long-run optimal
- \(v_\ast\) “takes into account the reward consequences of all possible future behavior”
- Expected long-term return is encoded into \(v_\ast\)
Optimal Policy \(\leftarrow\) Optimal Value
- Same for \(q_\ast(s,a)\) … in any state \(s\), choose the best action \(a\)
- Costs more to store \(q_\ast(s,a)\) than \(v_\ast(s)\)
- \(q_\ast\) encodes best action(s) without needing to know values of next states or environment dynamics \(p(s',r|s,a)\)
Bellman’s Eqations in Practice
\[ \begin{align} v_\ast(s) &= \max_a \sum_{s',r} \left[ r + \gamma v_\ast(s') \right]p(s',r|s,a) \\ q_\ast(s,a) &= \sum_{s',r} p(s',r|s,a)\left[ r + \gamma \max_{a'} q_\ast(s',a') \right] \end{align} \]
- Usually don’t know \(p(s',r|s,a)\)
- Usually can’t compute (sum and max too big)
- Markov property (assume this)