Background

• Illustrate trade-offs and issues arising in real applications
• How to incorporate domain knowledge
• Representation issues
• “Applications of reinforcement learning are still far from routine and typically require as much art as science.”

TD-Gammon

• Gerald Tesauro (1992-2002)
• Program: TD-Gammon
• Little knowledge of the game
• Played nearly as well as world champs
• Straightforward combination of TD(\(\lambda\)) and ANN for \(\hat{v}\)

Backgammon

• Complete knowledge of state is available
• Episodic
• Game tree has branching factor of 400 (much larger than Chess)
• Huge number of states

Setup

• Want \(\hat{v}(s,\mathbf{w})\) to estimate the probability of winning starting from state \(s\)
• Rewards are zero for all time steps except those on which a game is won (\(R_t=1\))

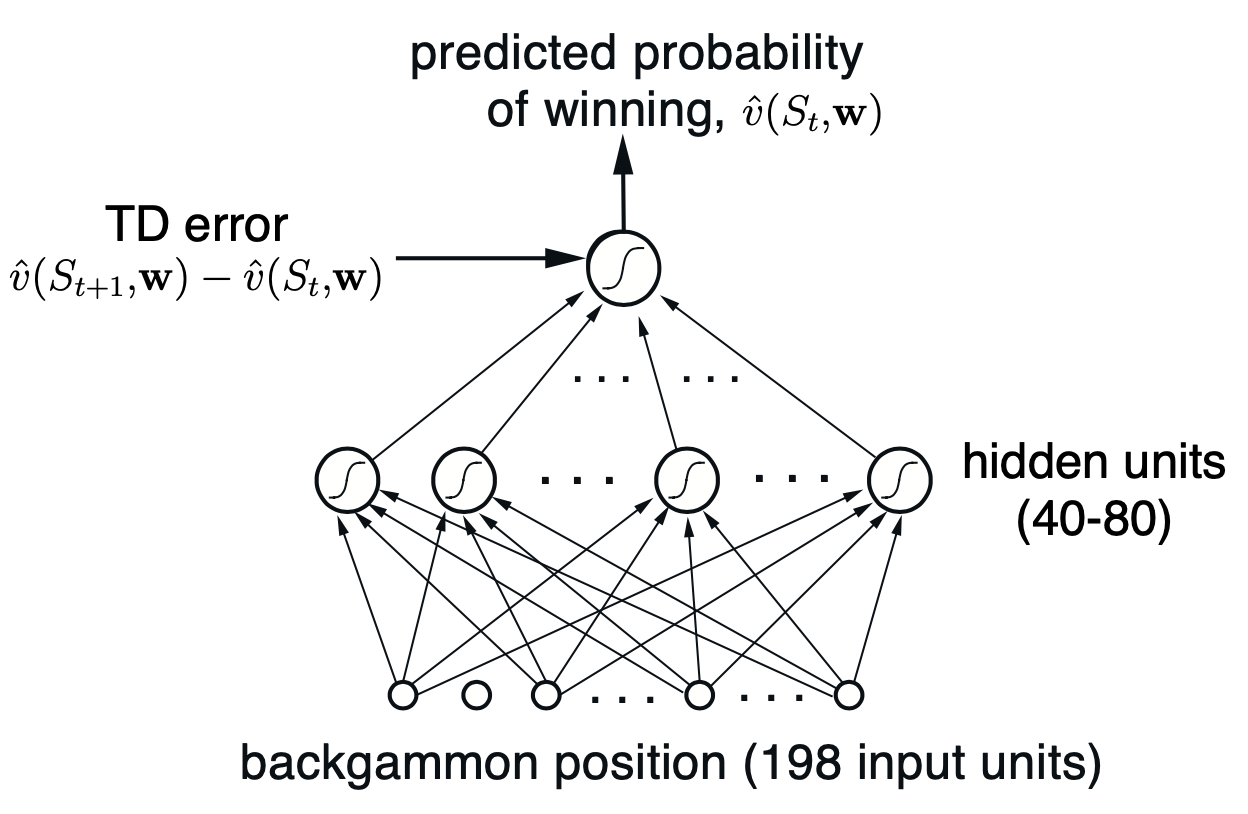
Setup

• Sigmoid activation function in ANN

• Board representation (pg. 423) - like a one-hot encoding

• Reward is zero except for a win

Learning

• Semi-gradient form of TD(\(\lambda\))
• Accumulating eligibility traces
• Play against itself (self-play)
• Used afterstates
• Initial games took 100,000 moves
• Performance improved rapidly

Performance

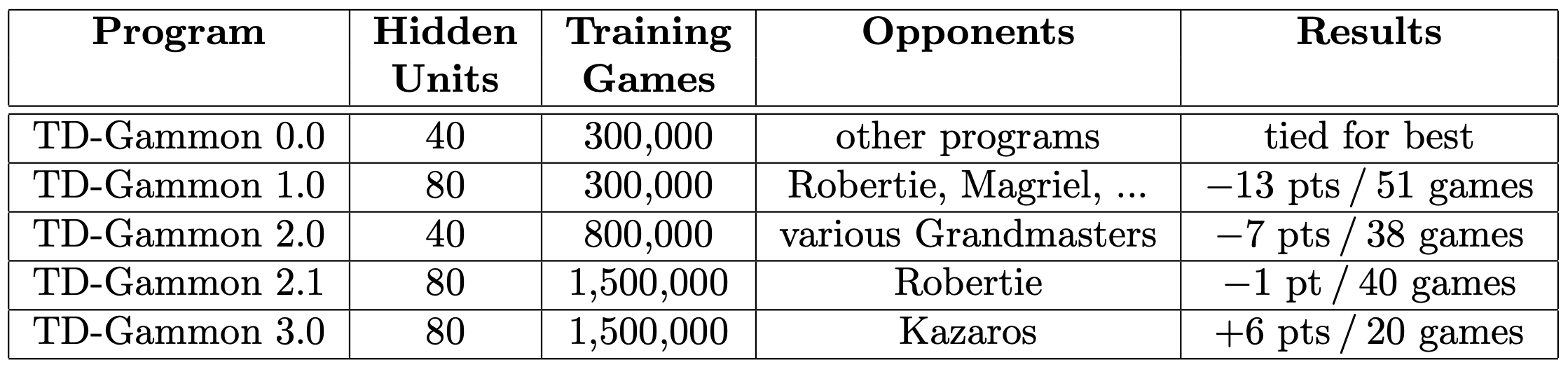
• After 300,000 games (episodes) TD-Gammon 0.0 played as well as any backgammon software, including Neurogammon also written by Tesauro which won a world tournament in 1989
• TD-Gammon 0.0 had essentially no knowledge of the game

TD-Gammon 1.0

• TG-Gammon 0.0 + backgammon features
• Gave human experts serious competition

TD-Gammon 2.x

• 2.0 used 40 hidden units
• 2.1 used 80 hidden units
• Look ahead search

TD-Gammon 3.x

• 3.0, 3.1 used 160 hidden units
• More advanced look ahead search
• More episodes
• Changed the way human experts play

Summary

Other Games

• Samuel’s Checkers Players
• Watson’s Daily-Double Wagering (Jeopardy!) - Adaptation of TD-Gammon system
• Optimizing memory control

Human Level Video Game Play

• How to represent and store value functions and/or policies?
• Features
  • Readily accessible
  • Convey information necessary for skilled performance
  • Often hand crafted based on human knowledge and intuition

Video Game Play

• ANN/DNN can learn task-relevant features
• Team at Google DeepMind developed deep Q-network (DQN)
• DQN = deep CNN + Q-learning
• Don’t need problem-specific feature sets
• Learned to play 49 different Atari 2600 video games
• Learned different policy for each game
• Same RL parameters and deep CNN architecture
• Achieved super-human performance on many games

Video Game Play

• ANN function approximation of action-value function
• Semi-gradient form of Q-learning
• Used experience replay
• Off-policy, \(\varepsilon\)-greedy policy
• 50 million frames = 38 days of experience
• No game-specific modifications to RL + ANN architecture

Policy ANN

Reward

• +1 when score increased
• -1 when score descrased
• 0 otherwise

Features

• Stack of four video frames

DQN Algorithm

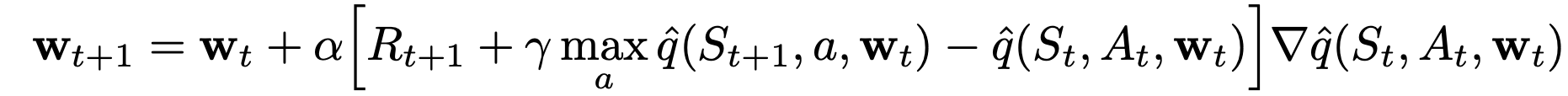
• Used mini-batch updates for the ANN (accumulate gradient over small batches before updating)
• RMSProp (use running average of gradients for weight updates … similar to eligibility traces)

Experience Replay

• Store \((S_t, A_t, R_{t+1}, S_{t+1})\) in replay memory
• At each time step (mini-batch) sample uniformly from replay memory
• Off-policy algorithm need not be applied along connected trajectories
• Data efficiency: Use each sample more than once
• Decorrelation: Breaks correlation among weight updates
• Stability: Experience (actions chosen) not dependent on current weights

DQN Modifications

• \(\gamma \max_a \hat{q}(S_{t+1},a,\mathbf{w}_t)\) target in DQN depends on the weights
• Can lead to oscillations and/or divergence
• Solution: Fix \(\mathbf{w}_t\) for some number, \(C\), of updates

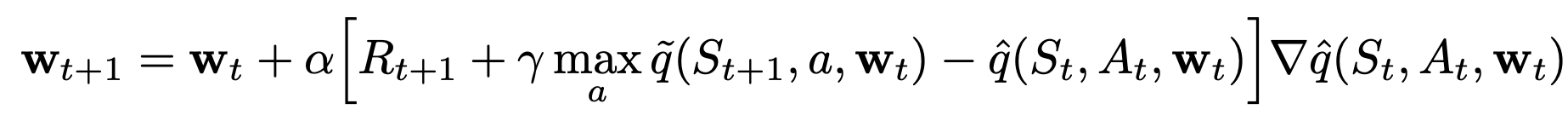
DQN Modifications (continued)

• Clip:

\[ \begin{gather} \delta_t = R_{t+1} + \gamma \max_a \tilde{q}(S_{t+1},a,\mathbf{w}) - \hat{q}(S_t,A_t,\mathbf{w}_t) \\ \mathbf{w}_{t+1} = \mathbf{w}_t + \alpha \text{clip}(\delta_t) \nabla \hat{q}(S_t,A_t,\mathbf{w}) \\ \text{clip}(\delta_t) = \begin{cases} +1, & \delta_t > +1 \\ \delta_t, & -1 \leq \delta_t \leq +1, \\ -1, & \delta_t < -1\end{cases} \end{gather} \]

DQN Summary

• Deep convolutional NN avoids the need for hand crafted features (features can be learned)
• Modifications led to significant benefits
  • Stacking frames to create Markovity
  • Experience replay
  • Freezing the learning target for \(C\) steps
  • Clipping the error
  • Mini-batches and gradient filtering
  • Deep (not shallow) NN

RL for Go

• Deep CNN to approximate value functions
• Supervised learning
• Monte Carlo tree search (MCTS)
• RL
• Self-play

Monte Carlo Tree Search (8.11)

• Effective for single-agent sequential decision problems
• Needs simple environment model for fast multistep simulation
• Used to select actions in a given state

MCTS

• Simulate many trajectories from current state to terminal state
• Extend trajectories that received high evaluations from earlier simulations
• Approximate value/policy functions not needed
• Trajectories generated using simple “rollout” policy
• MC estimate of \(q(s,a)\) for a small tree rooted at current state

MCTS

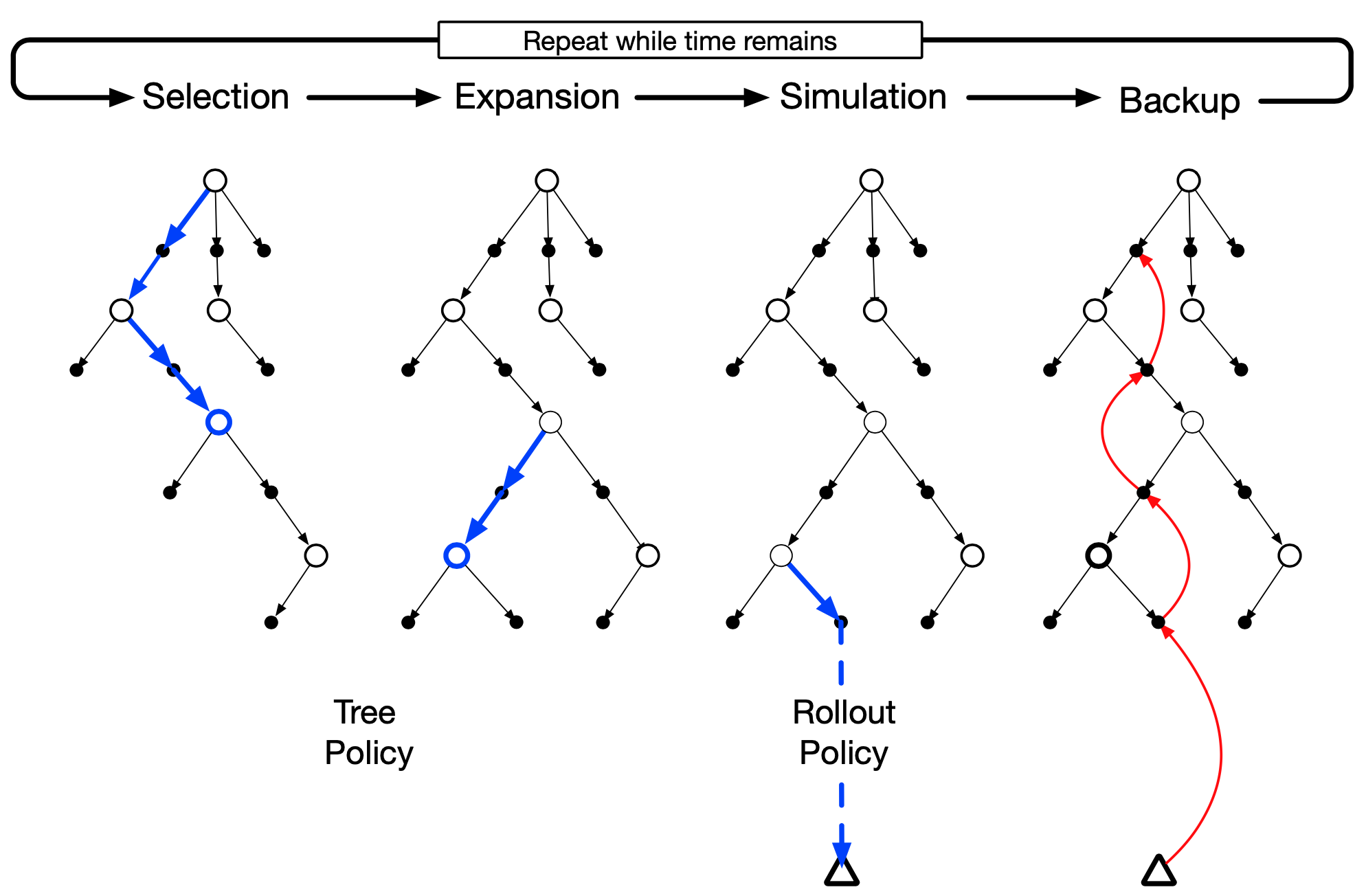
MCTS

• Outside tree: Rollout policy used for action selection
• Inside tree: Tree policy used for action selection
• Tree policy is \(\varepsilon\)-greedy on estimated \(q(s,a)\) function
• MCTS iteration
  • Select leaf node
  • Expand by adding child nodes (exploration)
  • Simulate to terminal state using rollout policy
  • Use backed up return to update/initialize \(q(s, a)\) at tree nodes

MCTS Summary

• Final action based on \(q\) or frequency of selection
• Discard (prune) unneeded portion of tree
• Grow a lookup table to store partial (not global table) \(q(s, a)\) for high-yielding sample trajectories
• No need for global \(q(s, a)\) function approximation
• Uses past experience to guide exploration

Rollout Algorithms (8.10): Overview

• Based on MC control applied to simulated trajectories rooted at current state
• Actions selected using “rollout” policy
• Returns averaged over many simulated trajectories
• Action selected based on max estimated value

Rollout Algorithms: Details

• MC estimate of \(q(s, a)\) only for current state \(s\) and for “rollout” policy
• Makes immediate use of \(q\) and then discards it
• Do not sample outcomes for every state-action pair
• No function approximation

Rollout Algorithms: Justification

• It is an explicit application of policy improvement
• Estimate \(q(s, a)\) for each \(a \in \mathcal{A}(s)\) and select the best action (greedy)
• This gives a better policy than the rollout policy

Alpha Go Zero

• Used no human data or guidance beyond basic rules of the game
• Learned from self-play RL
• Inputs/states were stone placements on game board
• Policy iteration: Policy eval + policy improvement
• (Read the book)

Alpha Go Zero