Chapter 13: Policy Gradient Methods
Jake Gunther
2020/20/2
Background
Background
- Past: Learned \(\hat{v}(s,\mathbf{w})\) or \(\hat{q}(s,a,\mathbf{w})\)
- Past: Policy was inferred from value function
- New: Learn parameterized policy \(\pi(a|s,\mathbf{\theta}) = \text{Pr}\{A_t=a|S_t=s,\mathbf{\theta}_t = \mathbf{\theta}\}\)
- Value functions may still be used to learn policy parameter
\[ \begin{gather} \mathbf{\theta} \in \mathbb{R}^{d'} \qquad (\text{policy parameter}) \\ \mathbf{w} \in \mathbb{R}^{d} \qquad (\text{value parameter}) \end{gather} \]
Policy Gradient Methods
- Update \(\mathbf{\theta}\) to maximize performance measure \(J(\mathbf{\theta})\)
- Gradient ascent:
\[ \mathbf{\theta}_{t+1} = \mathbf{\theta}_{t} + \alpha \widehat{\nabla J(\mathbf{\theta})} \]
where \(\widehat{\nabla J(\mathbf{\theta})}\) is a stochastic estimate in which
\[ E\{\widehat{\nabla J(\mathbf{\theta})}\} \approx \nabla J(\mathbf{\theta}) \]
Actor-Critic Methods
- Policy gradient methods: SGA on \(J(\mathbf{\theta})\) whether or not a value function is also learned
- Actor-critic methods: Learn both policy (actor) and value (critic) approximations
Advantages of Policy Approx.
Exploration vs. Exploitation
- To ensure exploration, require non-deterministic policy \(\pi(a|s,\mathbf{\theta}) \in (0,1)\)
- PG good for continuous action spaces
- Parameterized preferences \(h(s,a,\mathbf{\theta})\)
- Soft-max policy distribution
\[ \pi(a|s,\mathbf{\theta}) = \frac{e^{h(s,a,\mathbf{\theta})}}{\sum_b e^{h(s,b,\mathbf{\theta})}} \]
“soft-max in action preferences”
Parameterizations
- \(h(s,a,\mathbf{\theta})\) could be a DNN (as in AlphaGo)
- \(h(s,a,\mathbf{\theta}) = \mathbf{\theta}^T \mathbf{x}(s,a)\) or linear in features
Advantages of Policy Approx.
- \(\varepsilon\)-greed action selection leaves \(\varepsilon\) probability of random action
- Parameterized policy can approach a deterministic (optimal) policy to the extent allowed by the parameterization
- “Action-value methods have no natural way of finding stochast optimal policies…”
- “…whereas policy approximation methods can.”
Example 13.1 (page 323)
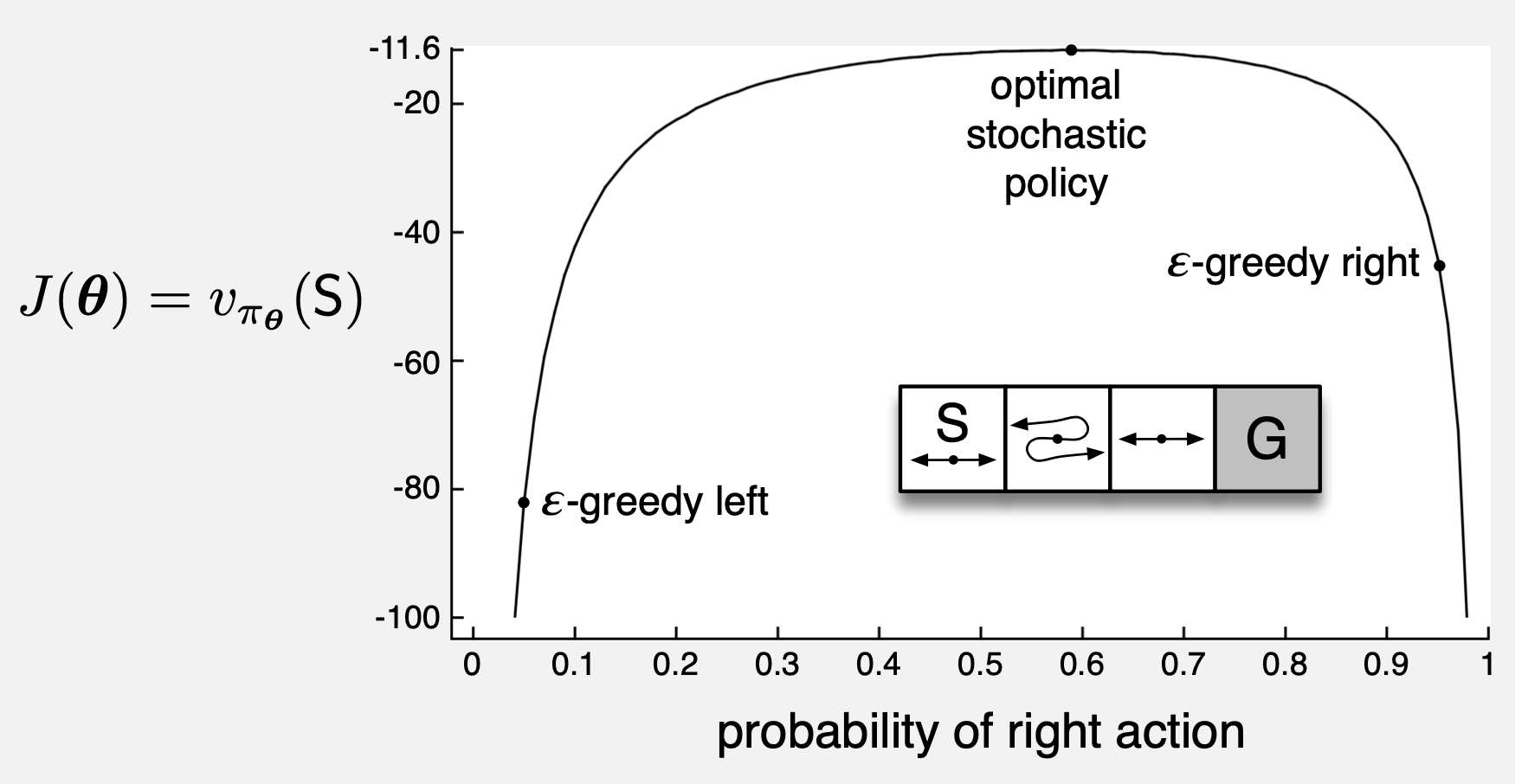
More Advantages
- The policy function may be a simpler function to approximate
- For some the action-value function is simpler and for others the policy function is simplier
- If policy is simpler, then PG will learn faster and yield superior asymptotic policy
- Policy methods offer good way to inject prior knowledge about form of policy into RL
Even More Advantages
- Policy approx.: Action probabilities change smoothly as function of \(\mathbf{\theta}\)
- Value approx.: Action values (\(\hat{v}\) and \(\hat{q}\)) change smoothly as a function of \(\mathbf{w}\), but \(\varepsilon\)-greedy policy may change dramatically for small change in value if that change results in a different action haveing maximal value
- Stronger convergence guarantees for PG
Policy Gradient Theorem
Policy Gradient Theorem
- In the episodic case: \(J(\mathbf{\theta}) = v_{\pi_\mathbf{\theta}}(s_0)\)
- Depends on:
- Action selections (depends on \(\mathbf{\theta}\))
- State distribution (depends on \(\mathbf{\theta}\))
- is straightforward to deal with: \((\mathbf{\theta},s_0) \rightarrow \text{actions}\)
- is hard because it depends on the environment which is unknown
- How can we estimate \(\widehat{\nabla J(\mathbf{\theta})}\)?
Policy Gradient Theorem
\[ \nabla J(\mathbf{\theta}) = C\cdot \sum_s \mu(s) \sum_a q_\pi(s,a) \nabla \pi(a|s,\mathbf{\theta}) \]


REINFORCE
All-Actions
\[ \begin{align} \nabla J(\mathbf{\theta}) &\propto \sum_s \mu(s) \sum_a q_\pi(s,a) \nabla \pi(a|s,\mathbf{\theta})\\ &= E\left[ \sum_a q_\pi(S_t,a)\nabla\pi(a|S_t,\mathbf{\theta})\right] \\ \mathbf{\theta}_{t+1} &= \mathbf{\theta} +\alpha \sum_a \hat{q}(S_t,a,\mathbf{w}) \nabla \pi(a,|S_t,\mathbf{\theta}) \end{align} \]
- Involves all actions (even ones not taken)
REINFORCE
\[ \begin{align} \nabla J(\mathbf{\theta}) &= E\left[ \sum_a q_\pi(S_t,a)\nabla\pi(a|S_t,\mathbf{\theta})\right] \\ &= E\left[ \sum_a \pi(a|S_t,\mathbf{\theta}) q_\pi(S_t,a)\frac{\nabla\pi(a|S_t,\mathbf{\theta})}{\pi(a|S_t,\mathbf{\theta})}\right] \\ &= E\left[ q_\pi(S_t,A_t)\frac{\nabla\pi(A_t|S_t,\mathbf{\theta})}{\pi(A_t|S_t,\mathbf{\theta})}\right] \end{align} \]
REINFORCE
\[ \begin{align} \nabla J(\mathbf{\theta}) &= E\left[ q_\pi(S_t,A_t)\frac{\nabla\pi(A_t|S_t,\mathbf{\theta})}{\pi(A_t|S_t,\mathbf{\theta})}\right] \\ &= E\left[ G_t\frac{\nabla\pi(A_t|S_t,\mathbf{\theta})}{\pi(A_t|S_t,\mathbf{\theta})}\right] \end{align} \]
REINFORCE Update
\[ \mathbf{\theta}_{t+1} = \mathbf{\theta} +\alpha G_t\frac{\nabla\pi(A_t|S_t,\mathbf{\theta})}{\pi(A_t|S_t,\mathbf{\theta})} \]
- Increases prob. of repeating \(A_t\) on future visits to \(S_t\)
- Favors actions that yield higher returns due to product with \(G_t\)
- \(\pi\) in denom. removes advantage of frequently selected actions
REINFORCE Algorithm

REINFORCE Example
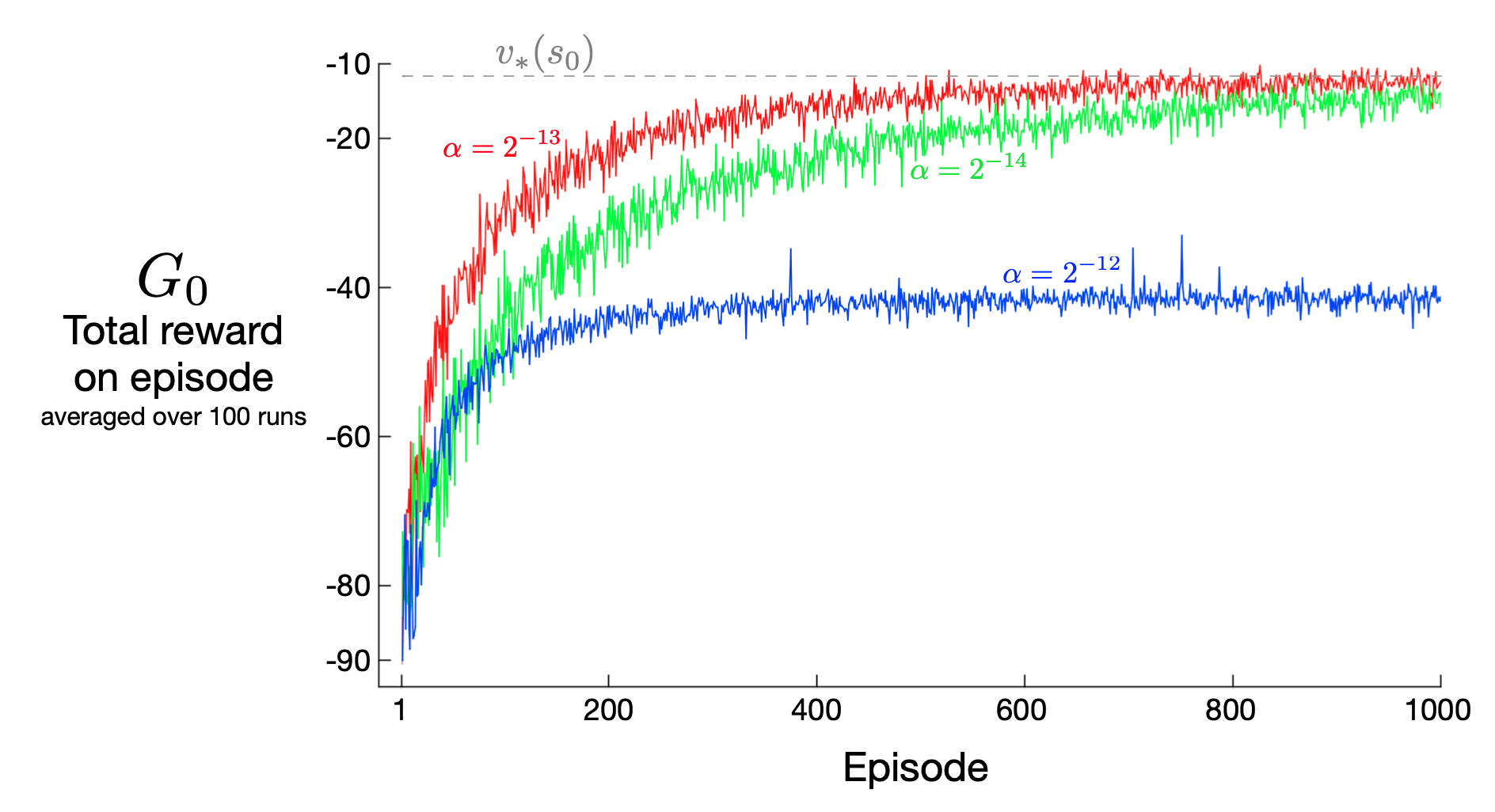
REINFORCE Performance
- High variance \(\rightarrow\) slow learning
REINFORCE with Baseline
Background
Policy Gradient Theorem
\[ \nabla J(\mathbf{\theta}) = C\cdot \sum_s \mu(s) \sum_a q_\pi(s,a) \nabla \pi(a|s,\mathbf{\theta}) \]
Policy Gradient with Baseline Theorem
\[ \nabla J(\mathbf{\theta}) = C\cdot \sum_s \mu(s) \sum_a \left(q_\pi(s,a)-b(s)\right) \nabla \pi(a|s,\mathbf{\theta}) \]
Proof
\[ \begin{align} \sum_a b(s) \nabla \pi(a|s,\mathbf{\theta}) &= b(s) \nabla \sum_a \pi(a|s,\mathbf{\theta}) \\ & = b(s) \nabla 1 = 0 \end{align} \]
Subtracting a baseline does nothing to the gradient
\[ \nabla J(\mathbf{\theta}) = C\cdot \sum_s \mu(s) \sum_a \left(q_\pi(s,a)-b(s)\right) \nabla \pi(a|s,\mathbf{\theta}) \]
REINFORCE with Baseline
\[ \mathbf{\theta}_{t+1} = \mathbf{\theta} +\alpha \left(G_t-b(S_t)\right)\frac{\nabla\pi(A_t|S_t,\mathbf{\theta})}{\pi(A_t|S_t,\mathbf{\theta})} \]
- Baseline does not change expectted value
- Baseline can reduce variance (speed learning)
- Could use \(b(s) = \hat{v}(s,\mathbf{w})\)
REINFORCE with Baseline

Performance
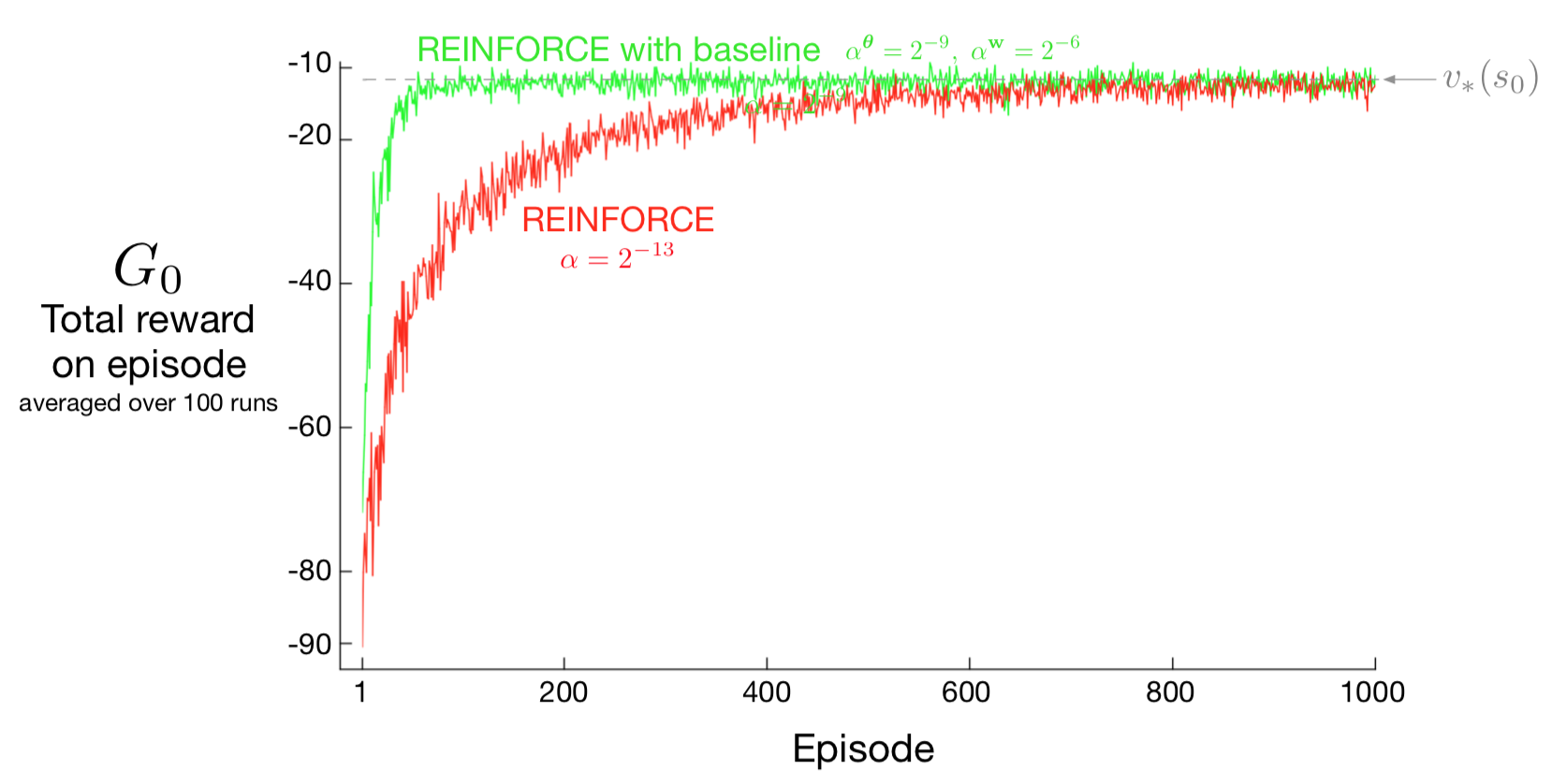
Actor-Critic Methods
Critic
- Approximated value function
- Approx. value function used for bootstrapping
- Updating the approx. value for \(s\) from approx. value for \(s'\)
- Bootstrapping \(\rightarrow\) bias & asymptotic dependence on quality of approximation
Actor-Critic Methods
- REINFORCE is Monte Carlo method
- Pro: unbaised
- Con: high variance, slow convergence, episodic
- Actor-Critic
- Temporal difference: online, fast convergence, continuing
- Multi-step methods: choose degree of bootstrapping
One-Step Actor-Critic
- Analog of TD(0), Sarsa(0), Q-learning
- Online, incremental, avoid eligibility traces
- Replace full return in REINFORCE with Baseline with one-step return and \(\hat{v}\) as baseline
(see equations on next page)
AC Update
\[ \begin{align} \mathbf{\theta}_{t+1} &= \mathbf{\theta}_t + \alpha \left( G_{t:t+1} -\hat{v}(S_t,\mathbf{w}) \right) \frac{\nabla \pi(A_t|S_t,\mathbf{\theta}_t)}{\pi(A_t|S_t,\mathbf{\theta}_t)} \\ &= \mathbf{\theta}_t + \alpha \left( R_{t+1} + \gamma \hat{v}(S_{t+1},\mathbf{w}) -\hat{v}(S_t,\mathbf{w}) \right) \frac{\nabla \pi(A_t|S_t,\mathbf{\theta}_t)}{\pi(A_t|S_t,\mathbf{\theta}_t)} \\ &= \mathbf{\theta}_t + \alpha \delta_t \frac{\nabla \pi(A_t|S_t,\mathbf{\theta}_t)}{\pi(A_t|S_t,\mathbf{\theta}_t)} \end{align} \]
One-Step AC Control

AC Control with Eligibility Traces

Policy Gradient for Continuing Problems
- Average rate of reward per time step \(r(\pi)\) (from chapter 10)
- Differential return \(G_t = R_{t+1} - r(\pi) + R_{t+2} - r(\pi) + \cdots\)
- Policy Gradient Theorem can be exteded to continuing case
- See book
Policy Parameterization for Continuous Actions
Background
- Till now “everything” assumed discrete & finite action spaces
- Policy \(\pi(a|s,\mathbf{\theta})\) had soft-max output “layer”
- To take action:
- Calculate probability \(\pi(a|s,\mathbf{\theta})\) for each \(a\in \mathcal{A}\)
- Draw random action from this distribution
- Q: What to do for large discrete or continuous action spaces?
- A: Learn statistics/parameters of the distribution
Gaussian Policy
\[ \begin{gather} \pi(a|s,\mathbf{\theta}) = \frac{1}{\sigma(s,\mathbf{\theta})\sqrt{2\pi}} \exp\left(-\frac{(a-\mu(s,\mathbf{\theta}))^2}{2\sigma(s,\mathbf{\theta})^2}\right) \\ \mu(s,\mathbf{\theta}) = \mathbf{\theta}_\mu^T \mathbf{x}_\mu(s) \qquad \sigma(s,\mathbf{\theta}) = \exp(\mathbf{\theta}_\sigma)^T \mathbf{x}_\sigma(s) \end{gather} \]
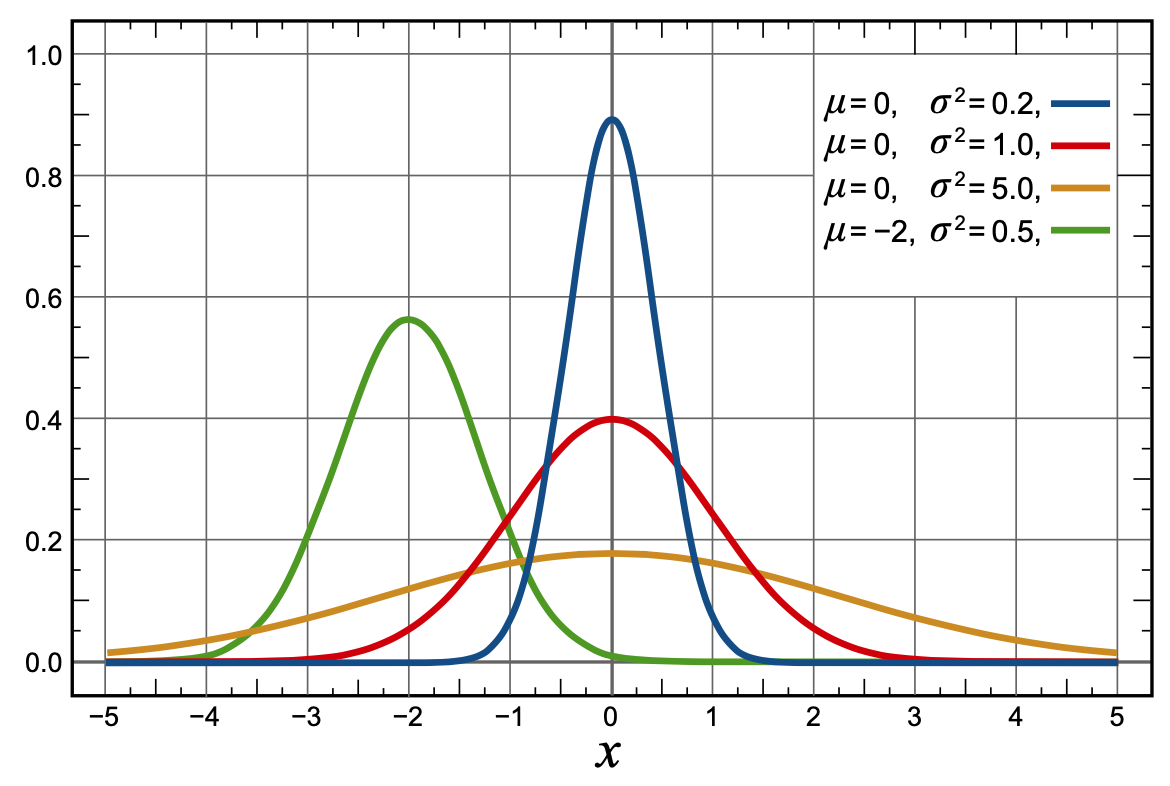
Comments