Paper Review
Jake Gunther
2020/3/4
The Paper
The Paper
“Proximal Policy Optimization Algorithms”
John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, Oleg Klimov
(OpenAI)
18 August 2017
Technical Contributions and Innovations
Claims
- PPO is simpler to implement than TRPO
- PPO is more general than TRPO
- PPO has lower sample complexity than TRPO
- PPO outperforms other policy gradient methods on benchmark tasks
Recent RL with DNN
- DQN
- “Vanilla” policy gradient methods
- Trust region / natural policy gradient methods
Problems with RL+DNN
- DQN works well for discrete action spaces but has not been shown to perform well on continuous control benchmarks
- “Vanilla” policy gradient methods have poor data efficiency and robustness
- TRPO is complicated and not compatible with DNNs using dropout or parameter sharing
Goals & Technical Ideas
- Data efficiency and reliable performance of TRPO
- Use first order optimization
- Novel objective function using clipped probability ratios
- Optimize lower bound of performance of policy
Background
Policy Gradient Methods Review
Recall REINFORCE and REINFORCE with baseline \[ \begin{align} \nabla J(\mathbf{\theta}) &= E\left[ q_\pi(S_t,A_t)\frac{\nabla\pi(A_t|S_t,\mathbf{\theta})}{\pi(A_t|S_t,\mathbf{\theta})}\right]\\ &= E\left[ \left(q_\pi(S_t,A_t)-v_\pi(S_t)\right)\frac{\nabla\pi(A_t|S_t,\mathbf{\theta})}{\pi(A_t|S_t,\mathbf{\theta})}\right] \end{align} \]
Advantage Function
Advantage function \(A(s, a) = q(s, a) - v(s)\) measures the improvement of action \(a\) compared to the average \(v(s) = \sum_a \pi(a|s)q(s, a)\).
If \(A(s,a)>0\), then gradient is pushed in that direction.
If \(A(s,a) <0\), then gradient is pushed in the opposite direction.
Aside
- We don’t want to have to approximate both \(q\) and \(v\) value functions
- Use TD error as an estimate for \(q\)
- \(A(s,a) = Q(s,a) - V(s) = R + \gamma V(s') - V(s)\)
- Two strategies:
- A2C (Advantage Actor Critic)
- A3C (Asynchronous Advantage Actor Critic)
Policy Gradient Methods Review
\[ L^{PG}(\theta) = \hat{E}\left[ \hat{A}_t \log \pi_\theta(a_t|s_t)\right], \qquad \hat{g} = \nabla_\theta L^{PG}(\theta) \]
where \(\hat{A}_t\) is an estimate of the advantage function and \(\hat{E}\) is empirical average of batch of samples.
Problem: Gradients of \(L^{PG}(\theta)\) can become destructively large. This is why we saw such small \(\alpha\) used with REINFORCE in book.
Trust Region Methods (TRPO)
Surrogate objective maximized subject to constraint on size of policy update \[ \begin{align} \max_\theta &\;\; \hat{E}_t\left( \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_\text{old}}(a_t|s_t)}\hat{A}_t\right) \\ \text{s.t.} &\;\; \hat{E}_t\left(\text{KL}[\pi_{\theta_\text{old}}(\cdot|s_t),\pi_\theta(\cdot|s_t)]\right) \leq \delta \end{align} \]
TRPO
Use a penalty instead of a constraint \[ \max_\theta\;\; \hat{E}_t\left( \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_\text{old}}(a_t|s_t)}\hat{A}_t - \beta\text{KL}[\pi_{\theta_\text{old}}(\cdot|s_t),\pi_\theta(\cdot|s_t)]\right) \]
Tuning \(\beta\) is problematic.
Clipped Surrogate Objective
\[ r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_\text{old}}(a_t|s_t)}, \qquad r_t(\theta_\text{old}) = 1 \]
Conservative policy iteration (CPI): \(L^\text{CPI}(\theta) = \hat{E}_t \left[ r_t(\theta) \hat{A}_t \right]\).
Without constraint maximizing CPI leads to large policy update.
PPO Objective Function
\[ L^\text{CLIP}(\theta) = \hat{E}_t\left[\min\left(r_t(\theta)A_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon\right)\hat{A}_t \right] \]
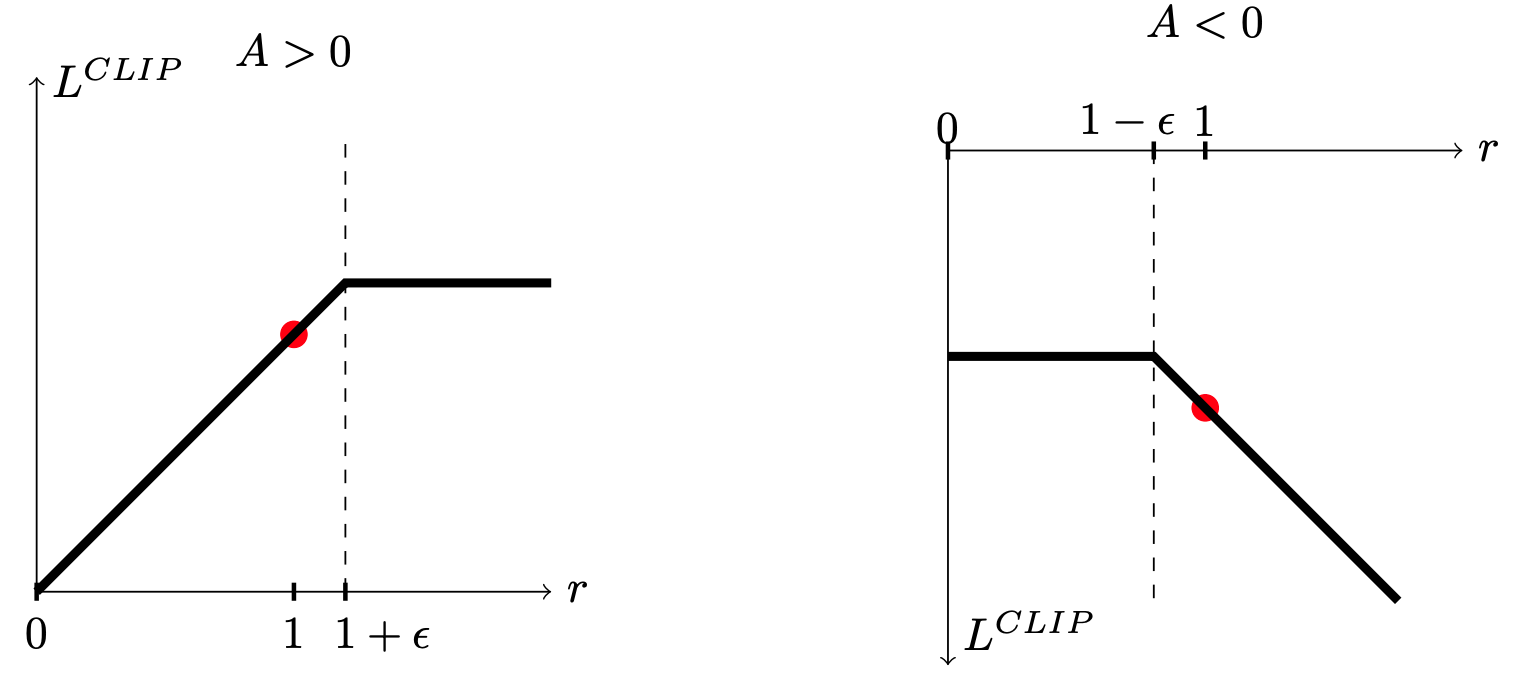
Clipping ratio removes the incentive for moving \(r_t\) outside interval \([1-\epsilon,1+\epsilon]\).
Intuition
- Red dot is starting point \(r=1\) for optimization on \(\theta\)
- Limit (clip) if objective increases too much
- Do nothing if objective decreases
- This optimizes a lower bound on \(L^\text{CPI}\)
PPO Clipped Objective
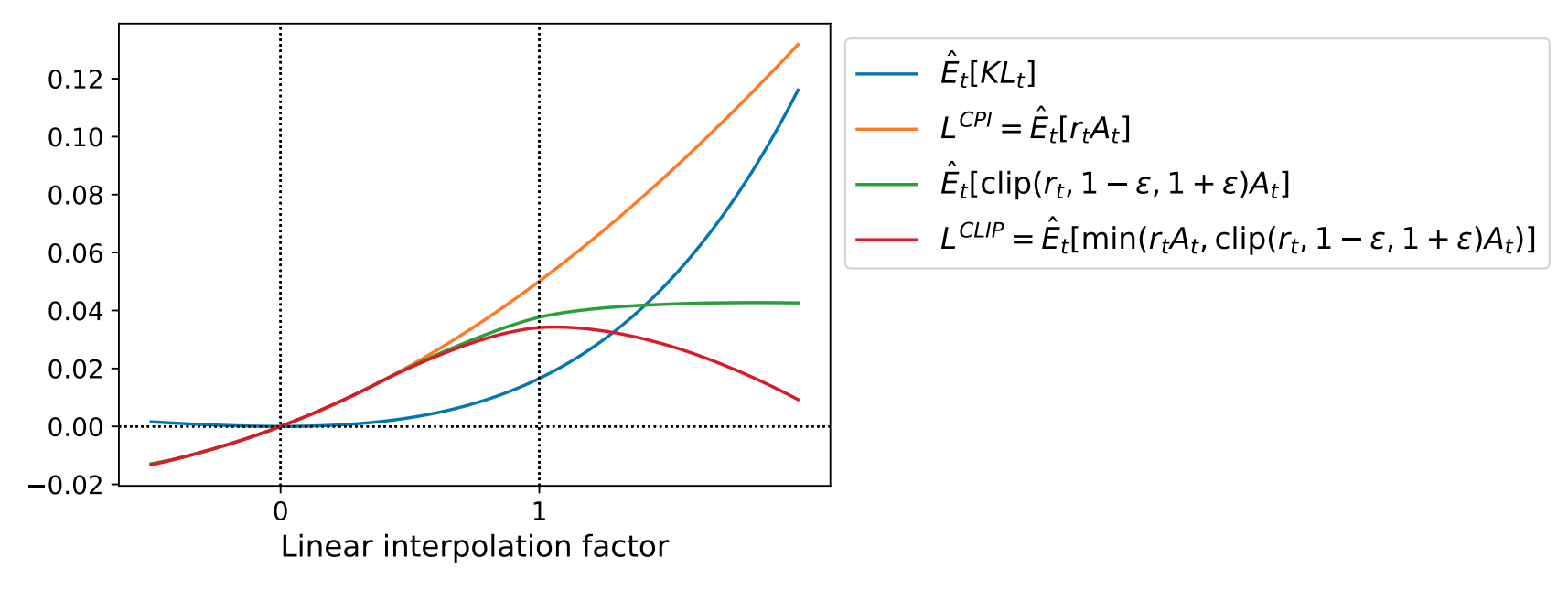
PPO Algorithm
\(N\) = number of instances of environment
Agent uses \(\pi_{\theta_\text{old}}\) in \(N\) different instances of env.
SGD or Adam on mini batches of data

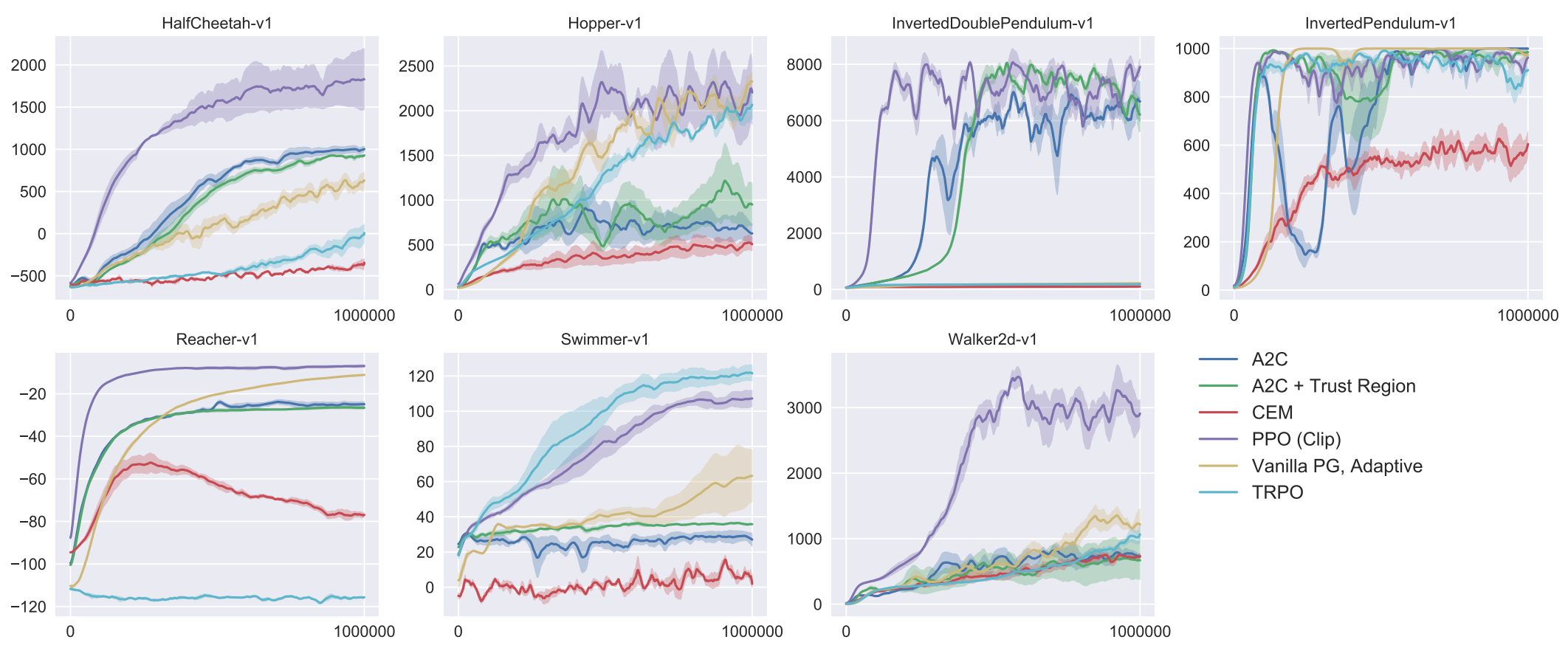
Simulation Results
Simulation Set 1
- Seven simulated robotics tasks in OpenAI Gym
- One million time steps
- Fully connected MLP with two hidden layers (64 units) and tanh activation
- Learned mean and variance of Gaussian distribution for continuous action policy
Simulation Set 1

Comparison with Other Algs.
Comparison with other algorithms considered to be effective for continuous action problems.
- TRPO
- Cross-entropy method (CEM)
- Vanilla policy gradient with adaptive step size
- A2C (Advantage Actor-Critic)
- A2C with trust region
PPO Wins!
Problem or Application Area
- Is the paper dedicated to learning for a particular task?
- Describe the nature of the problem or application being addressed in the paper? (Note: Theoretical papers may have no specific task in mind.)
Simulation Set 2
- Humanoid Running and Steering Showcase
- Humanoid robot: run, steer, and get up
- Tasks: forward locomotion, run to flag, run to flag under “cube fire”
Simulation Set 3
- Atari games (finite action space)