Maximum Margin Classifier

Suppose we are given samples $\{(\mathbf{x}_i,y_i)\}_{i=1}^N$ from two different classes, where $y_i \in \{+1,-1\}$ is the class label. The classification problem is to find a function that agrees with the class labels, $y_i f(\mathbf{x}_i) \geq 0$ for all $i$ . Here we consider only affine functions $f(\mathbf{x}) = \mathbf{a}^T\mathbf{x} + b$ . A classifier is a pair $(\mathbf{a},b)$ such that $y_i(\mathbf{a}^T\mathbf{x}_i + b) \geq 1$ .

Derivation

Given a vector $\mathbf{a}$ and samples $(\mathbf{u},+1)$ and $(\mathbf{v},-1)$ on the margins, we have

$\mathbf{a}^T \mathbf{u} + b = +1, \\ \mathbf{a}^T \mathbf{v} + b = -1.$

Subtracting yields

$\mathbf{a}^T(\mathbf{u} - \mathbf{v}) = 2,$

which will be used later.

The width of the slab may be computed as the length of the projected difference of $\mathbf{u}$ and $\mathbf{v}$ onto $\mathbf{a}$ ,

$\text{width} = \left\|\frac{\mathbf{a}\mathbf{a}^T(\mathbf{u}-\mathbf{v})}{\mathbf{a}^T\mathbf{a}}\right\| = \left\|\frac{\mathbf{a}}{\|\mathbf{a}\|} \frac{\mathbf{a}^T(\mathbf{u}-\mathbf{v})}{\|\mathbf{a}\|} \right\| = \frac{\mathbf{a}^T(\mathbf{u}-\mathbf{v})}{\|\mathbf{a}\|} = \frac{2}{\|\mathbf{a}\|}.$

The margin is half of the slab width

$\text{margin} = \frac{1}{\|\mathbf{a}\|}.$

Thus, maximizing the margin is equivalent to minimizing $\|\mathbf{a}\|$ . The maximum margin classifier may be obtained by solving

$\text{minimize} \;\|\mathbf{a}\| \quad \text{subject to} \quad y_i(\mathbf{a}^T \mathbf{x}_i + b) \geq 1, \;\;\forall i.$

When the samples are not separable by a hyperplane, we may introduce non-negative variables $e_i$ to relax the constraints

$y_i (\mathbf{a}^T \mathbf{x}_i + b) \geq 1 - e_i, \;\;\forall i.$

We want to minimize the extent to which the original constraints are violated. This leads to the modified problem

$\text{minimize} \;\|\mathbf{a}\| +\gamma \mathbf{1}^T \mathbf{e} \quad \text{subject to} \quad y_i(\mathbf{a}^T \mathbf{x}_i + b) \geq 1-e_i, \quad e_i \geq 0 \;\;\forall i.$

A closely related problem is

$\text{minimize} \;\frac{1}{2}\|\mathbf{a}\|^2 +\gamma \mathbf{1}^T \mathbf{e} \quad \text{subject to} \quad y_i(\mathbf{a}^T \mathbf{x}_i + b) \geq 1-e_i, \quad e_i \geq 0 \;\;\forall i.$

Show that the dual of the first problem is given by

$\text{maximize} \;\mathbf{1}^T\boldsymbol{\lambda} \quad \text{subject to} \quad \boldsymbol{\lambda}\geq \mathbf{0}, \quad \boldsymbol{\mu}\geq \mathbf{0}, \\ \quad\left\|\sum_i \lambda_i y_i \mathbf{x}_i \right\|_2 \leq 1, \quad \boldsymbol{\lambda} + \boldsymbol{\mu} = \gamma\mathbf{1}, \quad \boldsymbol{\lambda}^T\mathbf{y} = 0,$

and the dual of the second problem is given by

$\text{maximize} \;\mathbf{1}^T\boldsymbol{\lambda} -\frac{1}{2} \sum_i \sum_j \lambda_i \lambda_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j \quad \text{subject to} \quad \boldsymbol{\lambda}\geq \mathbf{0}, \quad \boldsymbol{\mu}\geq \mathbf{0}, \\ \boldsymbol{\lambda} + \boldsymbol{\mu} = \gamma\mathbf{1}, \quad \boldsymbol{\lambda}^T\mathbf{y} = 0.$

In both cases show that the optimal $\mathbf{a}$ is a weighted linear combination of the data $\mathbf{x}_i$ ,

$\mathbf{a} = \sum_i \lambda_i y_i \mathbf{x}_i.$

Substituting this expression for $\mathbf{a}$ into $f(\mathbf{x}) = \mathbf{a}^T \mathbf{x} + b$ gives the classification function

$f(\mathbf{x}) = \sum_i \lambda_i y_i \mathbf{x}_i^T \mathbf{x} + b.$

Kernel Functions

Notice that everywhere that a test vector $\mathbf{x}$ or training vector $\mathbf{x}_i$ appears in the dual objective function or in the classification function, it appears as an inner product. Skipping a lot of background material, it is common to replace the inner product $\mathbf{x}_i^T \mathbf{x}$ by the kerlnel function $K(\mathbf{x}_i,\mathbf{x})$ . Popular kernels for classification include the following examples.

$\text{linear:} \;\;K(\mathbf{x}_i,\mathbf{x}) = \mathbf{x}_i^T\mathbf{x},\\ \text{$d$th-degree polynomial:} \;\;K(\mathbf{x}_i,\mathbf{x}) = (1+\mathbf{x}_i^T\mathbf{x})^d,\\ \text{radial basis:} \;\;K(\mathbf{x}_i,\mathbf{x}) = \exp(-\gamma \|\mathbf{x}_i - \mathbf{x}\|^2),\\ \text{neural network:}\;\;K(\mathbf{x}_i,\mathbf{x})=\tanh(\kappa_1 \mathbf{x}_i^T \mathbf{x} + \kappa_2).$

The evaluation of many kernel functions is equivalent to promoting $\mathbf{x}$ to a higher dimension through a nonlinear mapping, and then evaluating the inner product in that higher dimensional space. This is advantageous becuase data that is not separable in its native format may be linearly separable in a higher dimensional space.

Substituting the kernel function into the objective function leads to the following optimization problem.

$\text{maximize} \;\mathbf{1}^T\boldsymbol{\lambda} -\frac{1}{2} \sum_i \sum_j \lambda_i \lambda_j y_i y_j K(\mathbf{x}_i,\mathbf{x}_j) \quad \text{subject to} \quad \boldsymbol{\lambda}\geq \mathbf{0}, \quad \boldsymbol{\mu}\geq \mathbf{0}, \\ \boldsymbol{\lambda} + \boldsymbol{\mu} = \gamma\mathbf{1}, \quad \boldsymbol{\lambda}^T\mathbf{y} = 0$

$\text{maximize} \;\mathbf{1}^T\boldsymbol{\lambda} -\frac{1}{2} \boldsymbol{\lambda}^T \mathbf{M} \boldsymbol{\lambda} \quad \text{subject to} \quad \boldsymbol{\lambda}\geq \mathbf{0}, \quad \boldsymbol{\mu}\geq \mathbf{0}, \\ \boldsymbol{\lambda} + \boldsymbol{\mu} = \gamma\mathbf{1}, \quad \boldsymbol{\lambda}^T\mathbf{y} = 0,$

where $\mathbf{M} = \text{diag}(\mathbf{y}) \, \mathbf{K}\, \text{diag}(\mathbf{y})$ and $\mathbf{K}$ is the $N \times N$ matrix with entries $[\mathbf{K}]_{i,j} = K(\mathbf{x}_i,\mathbf{x}_j)$ .

It also leads to the classifier

$f(\mathbf{x}) = \sum_i \lambda_i y_i K(\mathbf{x}_i,\mathbf{x}) + b.$

Barrier Method

Using the barrier method, the inequality constraints can be incorporated into the objective function as follows,

$\text{minimize} \; \frac{t}{2} \boldsymbol{\lambda}^T \mathbf{M} \boldsymbol{\lambda}-t\mathbf{1}^T\boldsymbol{\lambda} - \sum_{i=1}^N \log(\lambda_i) - \sum_{i=1}^N \log(\mu_i) \quad \text{subject to} \quad \boldsymbol{\lambda} + \boldsymbol{\mu} = \gamma\mathbf{1}, \quad \boldsymbol{\lambda}^T\mathbf{y} = 0.$

The Lagrangian for this problem is

$L(\boldsymbol{\lambda},\boldsymbol{\mu}) = \frac{t}{2} \boldsymbol{\lambda}^T \mathbf{M} \boldsymbol{\lambda}-t\mathbf{1}^T\boldsymbol{\lambda} - \sum_{i=1}^N \log(\lambda_i) - \sum_{i=1}^N \log(\mu_i)+\boldsymbol{\nu}^T \left( \boldsymbol{\lambda} + \boldsymbol{\mu} - \gamma\mathbf{1}\right) + \omega \boldsymbol{\lambda}^T\mathbf{y}.$

The KKT equations are as follows:

$\text{(dual feasibility)} \qquad \nabla_{\begin{bmatrix}\boldsymbol{\lambda}\\ \boldsymbol{\mu}\end{bmatrix}} L(\boldsymbol{\lambda},\boldsymbol{\mu}) = \mathbf{0}, \quad \Rightarrow \quad \begin{split} t\mathbf{M} \boldsymbol{\lambda} - t \mathbf{1} - \mathbf{1}./\boldsymbol{\lambda} + \boldsymbol{\nu} + \omega \mathbf{y} = \mathbf{0}, \\ -\mathbf{1}./\boldsymbol{\mu} + \boldsymbol{\nu} = \mathbf{0}, \end{split} \\ \text{(primal feasibility)} \qquad \begin{split} \boldsymbol{\lambda} + \boldsymbol{\mu} = \gamma\mathbf{1}, \\ \boldsymbol{\lambda}^T\mathbf{y} = 0. \end{split}$

Newton's Method

Using the first order Taylor approximation for the inverse function

$\frac{1}{x + \Delta x} \approx \frac{1}{x} - \frac{\Delta x}{x^2},$

substitution $(\boldsymbol{\lambda},\boldsymbol{\mu}) \rightarrow (\boldsymbol{\lambda}+\boldsymbol{\Delta \lambda},\boldsymbol{\mu} + \boldsymbol{\Delta \mu})$ into the KKT equations and linearize to obtain

$t\mathbf{M} \boldsymbol{\lambda} + t\mathbf{M} \boldsymbol{\Delta \lambda}- t \mathbf{1} - \mathbf{1}./\boldsymbol{\lambda} + \text{diag}(\mathbf{1}./\boldsymbol{\lambda}^2)\boldsymbol{\Delta\lambda} + \boldsymbol{\nu} + \omega \mathbf{y} = \mathbf{0}, \\ -\mathbf{1}./\boldsymbol{\mu} + \text{diag}(\mathbf{1}./\boldsymbol{\mu}^2)\boldsymbol{\Delta \mu} + \boldsymbol{\nu} = \mathbf{0}, \\ \boldsymbol{\lambda} +\boldsymbol{\Delta\lambda}+ \boldsymbol{\mu} + \boldsymbol{\Delta\mu} = \gamma\mathbf{1}, \\ \mathbf{y}^T\boldsymbol{\lambda} + \mathbf{y}^T\boldsymbol{\Delta\lambda} = 0.$

Rewrite these quations in matrix-vector form to obtain,

$\begin{bmatrix} t\mathbf{M} + \text{diag}(\mathbf{1}./\boldsymbol{\lambda}^2) & \mathbf{0} & \mathbf{I} & \mathbf{y} \\ \mathbf{0} & \text{diag}(\mathbf{1}./\boldsymbol{\mu}^2) & \mathbf{I} & \mathbf{0} \\ \mathbf{I} & \mathbf{I} & \mathbf{0} & \mathbf{0} \\ \mathbf{y}^T & \mathbf{0} & \mathbf{0} & \mathbf{0} \end{bmatrix} \begin{bmatrix} \boldsymbol{\Delta \lambda} \\ \boldsymbol{\Delta \mu} \\ \boldsymbol{\nu} \\ \omega \end{bmatrix} = -\begin{bmatrix} t\mathbf{M}\boldsymbol{\lambda} - t\mathbf{1} - \mathbf{1}./\boldsymbol{\lambda} \\ -\mathbf{1}./\boldsymbol{\mu} \\ \boldsymbol{\lambda}+\boldsymbol{\mu} - \gamma\mathbf{1} = \mathbf{0} \\ \mathbf{y}^T\boldsymbol{\lambda} = 0, \end{bmatrix}$

where the assumption that $(\boldsymbol{\lambda},\boldsymbol{\mu})$ are primal feasible was used. A feasible point must satisfy

$\boldsymbol{\lambda} + \boldsymbol{\mu} = \gamma \mathbf{1},\quad \mathbf{y}^T\boldsymbol{\lambda} = 0, \quad \boldsymbol{\lambda} \geq \mathbf{0}, \quad\boldsymbol{\mu} \geq \mathbf{0}.$

This can be achieved by observing the following,

$\mathbf{y}^T \boldsymbol{\lambda} = \sum_{i=1}^N y_i \lambda_i \\ =\sum_{i: y_i=+1} \lambda_i - \sum_{i:y_i=-1} \lambda_i \\ = 0$

provided

$\sum_{i:y_i=+1} \lambda_i = \sum_{i:y_i=-1} \lambda_i.$

Observing that $\lambda_i \geq 0, \mu_i\geq 0$ and $\lambda_i + \mu_i = \gamma$ , define

$m = \sum_{i:y_i=+1} 1, \qquad n=\sum_{i:y_i=-1} 1,$

and set

$\lambda_i = \begin{cases} \gamma/m, & y_i=+1, \\ \gamma/n, & y_i=-1,\end{cases} \qquad \mu_i = \begin{cases} \gamma(m-1)/m, & y_i=+1, \\ \gamma(n-1)/n, & y_i=-1,\end{cases}$

then $(\boldsymbol{\lambda},\boldsymbol{\mu})$ is primal feasible. Of course other initializations are possible. It's a big feasible set!

Algorithm

blah, blah, blah ...

Block Gaussian Elimination

blah, blah, blah ...

Assignment

Do the following:

Write code to solve the quadratic program (QP) above with inequality and equality constraints.
Use the linear kernel and demonstrate 100% correct classification on the linearly separable dataset. Use plots to show the dataset, the classifer function, the margins, and the support vectors.
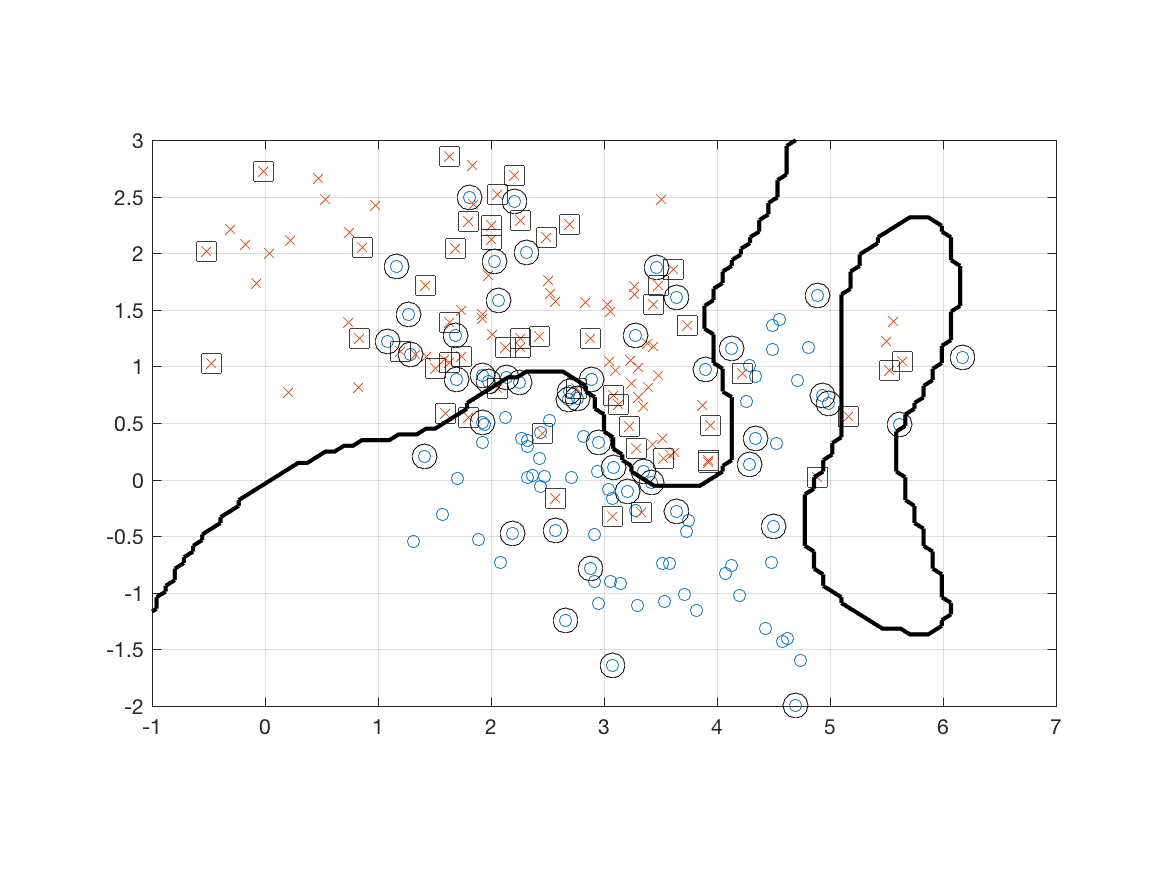
Use the linear kernel on the mixture dataset. Use plots to show the dataset, the classifer function, the margins, and the support vectors. What is the classification error rate on the training dataset?
Use the radial basis function kernel on the mixture dataset. Use plots to show the dataset, the classifer function, the margins, and the support vectors. What is the classification error rate on the training dataset?
Use the linear kernel on the digits dataset. (Only classify digits "0" and "1".) Are the training data linearly separable. What is the classification error rate on the training and test sets?
Use the radial basis function kernel on the digits dataset. Are the training data separable in this case? What is the classification error rate on the training and test sets?

Datasets

Linearly separable data (two-dimensional data). Dataset1, dataset2.
Mixture data (two-dimensional data) (from The Elements of Statistical Learning) Mixture set.
Digits (256-dimensional data) (from The Elements of Statistical Learning) Train, test.

Note: Tables of data in text files can be loaded into Matlab using the command a = textread('train.txt');, for example. In the digits data, the file format is as follows. Each row corresponds to a digit. The first element is the digit, an integer between 0 and 9, inclusive. The next 256 elements are the grayscale pixel values in a 16 x 16 image of the digit in row scanned order.

 
xxxxxxxxxx
a = textread('train.txt'); % Load the digits database from file.
[num_digits,nc] = size(a); % How many digits are in the database?
i = 200; % Select an image to view.
d = a(i,1); % Get the digit.
p = reshape(a(i,1+[1:256]),16,16).'; % Reshape the pixel data to an image.
imagesc(p); axis image; shg; % Show an image of the digit.
disp(sum(a(:,1)==0)); % How many zeros are there in the database?
disp(sum(a(:,1)==5)); % How many fives are in the database?
% And so on...

Results

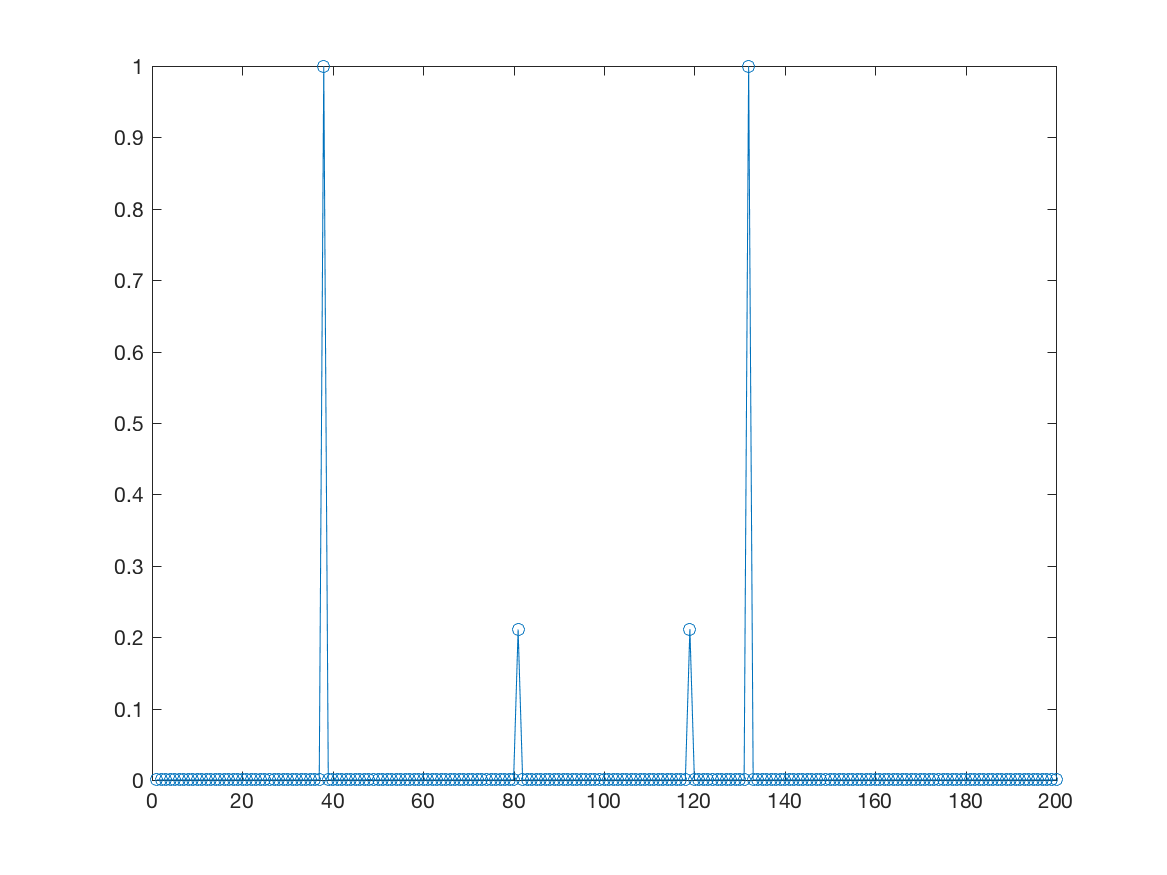
For the linearly separable dataset using the linear kernel, the separation is shown below for $\gamma = 10$ . The red line is the $\mathbf{a}$ vector and the blue line is the line $\mathbf{a}^T \mathbf{x} + b = 0$ . This is the separating hyperplane. The dashed blue lines are the separating hyperplane shifted by plus and minus the margin. solution

A plot of the lagrange multipliers $\boldsymbol{\lambda}$ is shown below. Notice that only three values are non-zero. These correspond to the support vectors. lambda

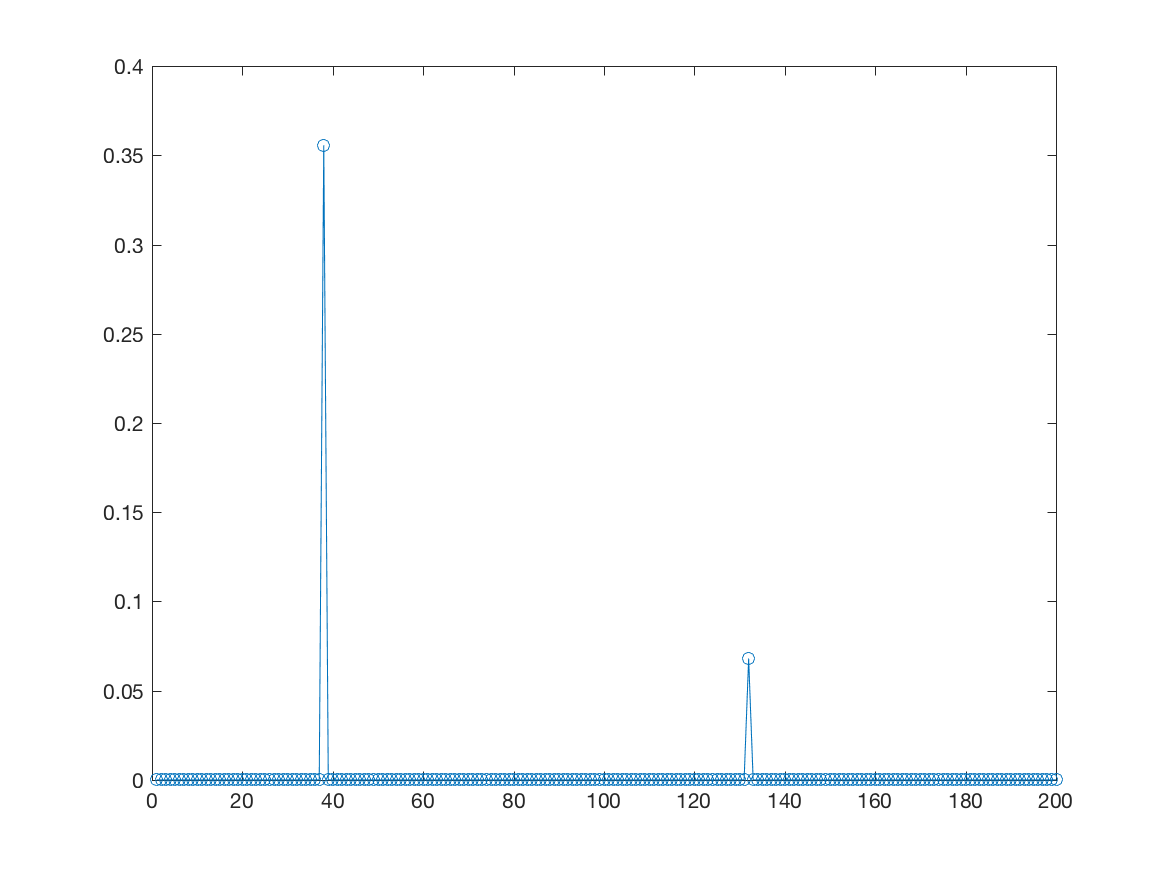
I re-solved the problem with $\gamma = 1$ . The results are shown below. Notice that with less weight on keeping the errors small, a two of the samples fall into the margin area. solution

Here is a plot of the $\boldsymbol{\lambda}$ vector. solution

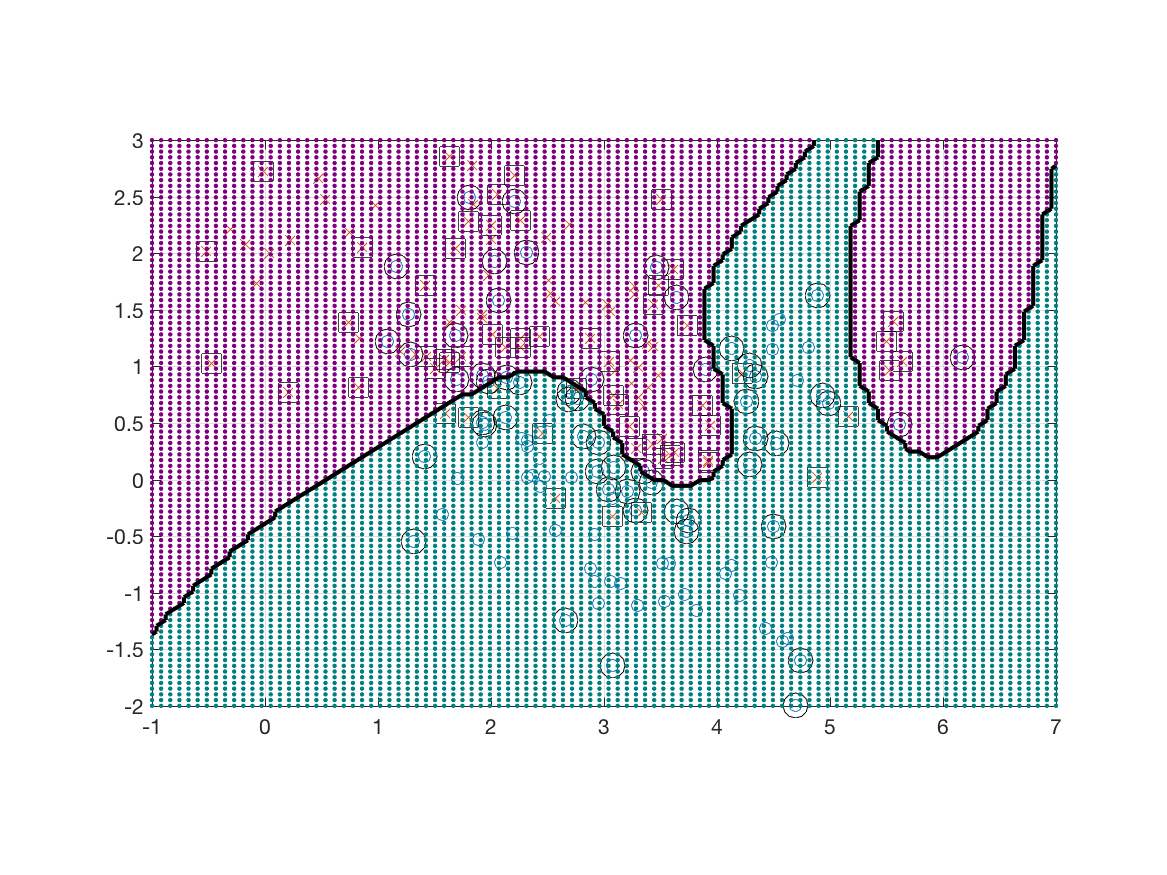
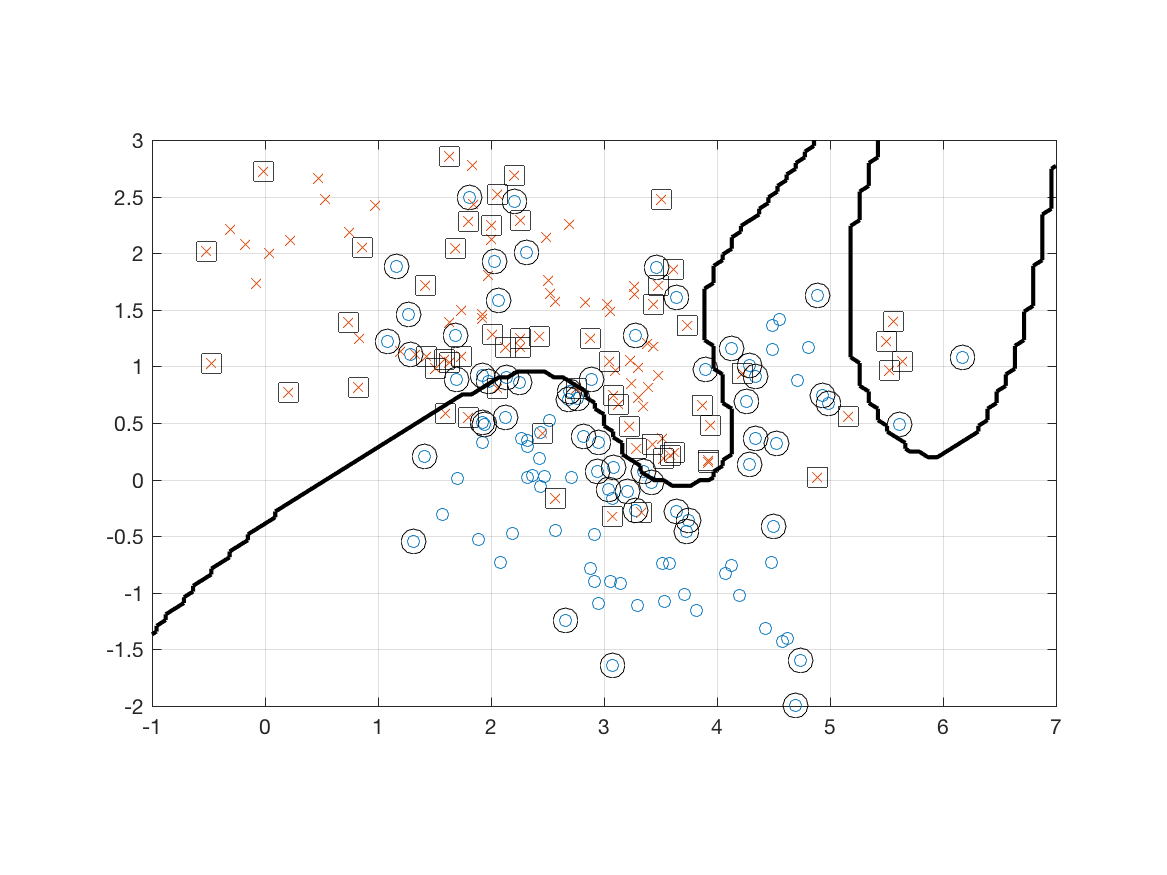
Here is a plot of the $\mathbf{e}$ vector. The error is positive for those two samples that fall into the margin slab. solution

Next I loaded the mixture dataset and used the radial basis function kernel. The results for $\gamma=10$ are shown below. solution

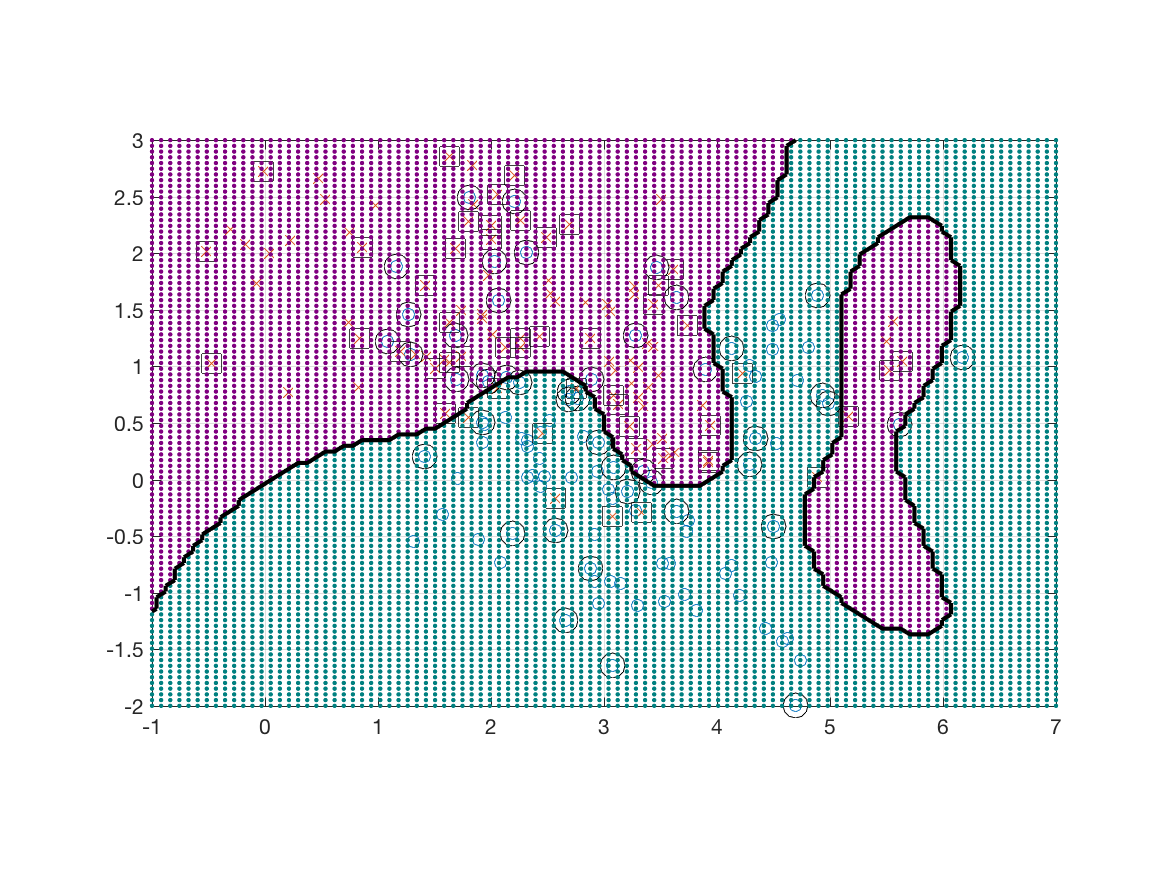
To prove that it is working, I evaluated the learned classifier at 10,000 test points and used color to encode the decisions in the figure below. solution

And here are the results when $\gamma = 1$ . solution

Here are 10,000 test points. solution