Discrete-Time Signals Questions

1. Consider the signal

   $$\begin{array}{}\text{(1)}& \begin{array}{c}f[n]=\left[\begin{array}{c}x[n]\\ y[n]\\ z[n]\end{array}\right]\end{array}\end{array}$$

   where $x[n],y[n],z[n]$$x[n], y[n], z[n]$ come from a 3-axis accelerometer as shown below

   What is the dimension? What is the number of channels?

2. Let a signal be defined as follows:

where $x[n]$$x[n]$ and $y[n]$$y[n]$ are plotted in the figure below.

Characterize this signal in terms of:

• Domain (continuous or discrete)

• Range (continuous or discrete)

• Dimension (number of independent variables)

• Channels (number of dependent variables)

By the way, when the $(x[n],y[n])$$(x[n],y[n])$ coordinates are connected as in a line drawing, you get the following picture.

And that is reminiscent of this photograph.

As we expect for a discrete-time signal, the values in this two-channel sequence could be recorded in a table. In this case, there are 1887 sample pairs in this sequence. The signal is not defined for $n<0$$n<0$ or for $n\ge 1887$$n\geq 1887$. Therefore this is a finite length signal.

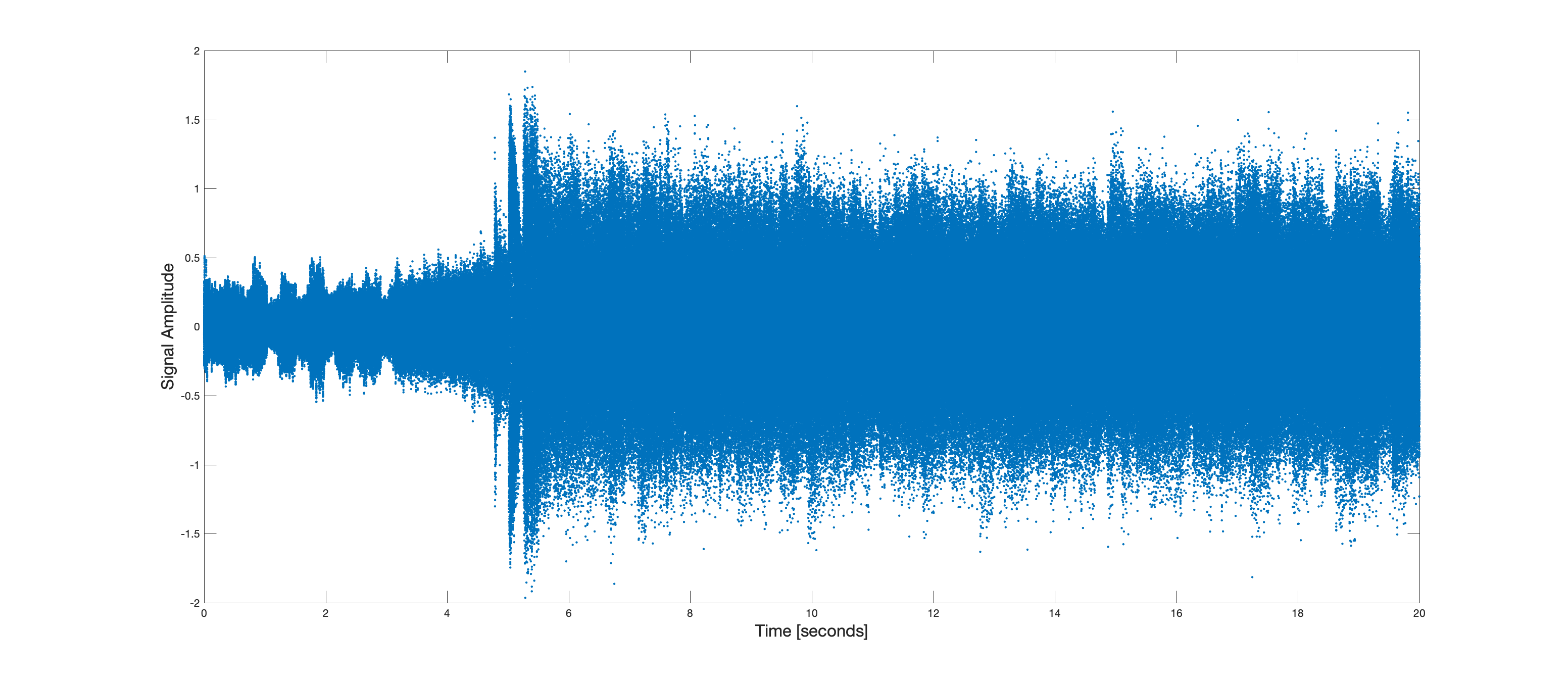
2. Consider the signal waveform pictured below in which the samples $x[n]$$x[n]$ are indicated by points. The horizontal axis has been scaled to reflect true time with units of seconds. This is a 20 second long segment of a longer signal.

You can hear the audio by clicking here and the slow version. This is the song "Language" by Porter Robinson. You can listen to the full song on YouTube.

Characterize this signal in terms of:

• Domain (continuous or discrete)

• Range (continuous or discrete)

• Dimension (number of independent variables)

• Channels (number of dependent variables)

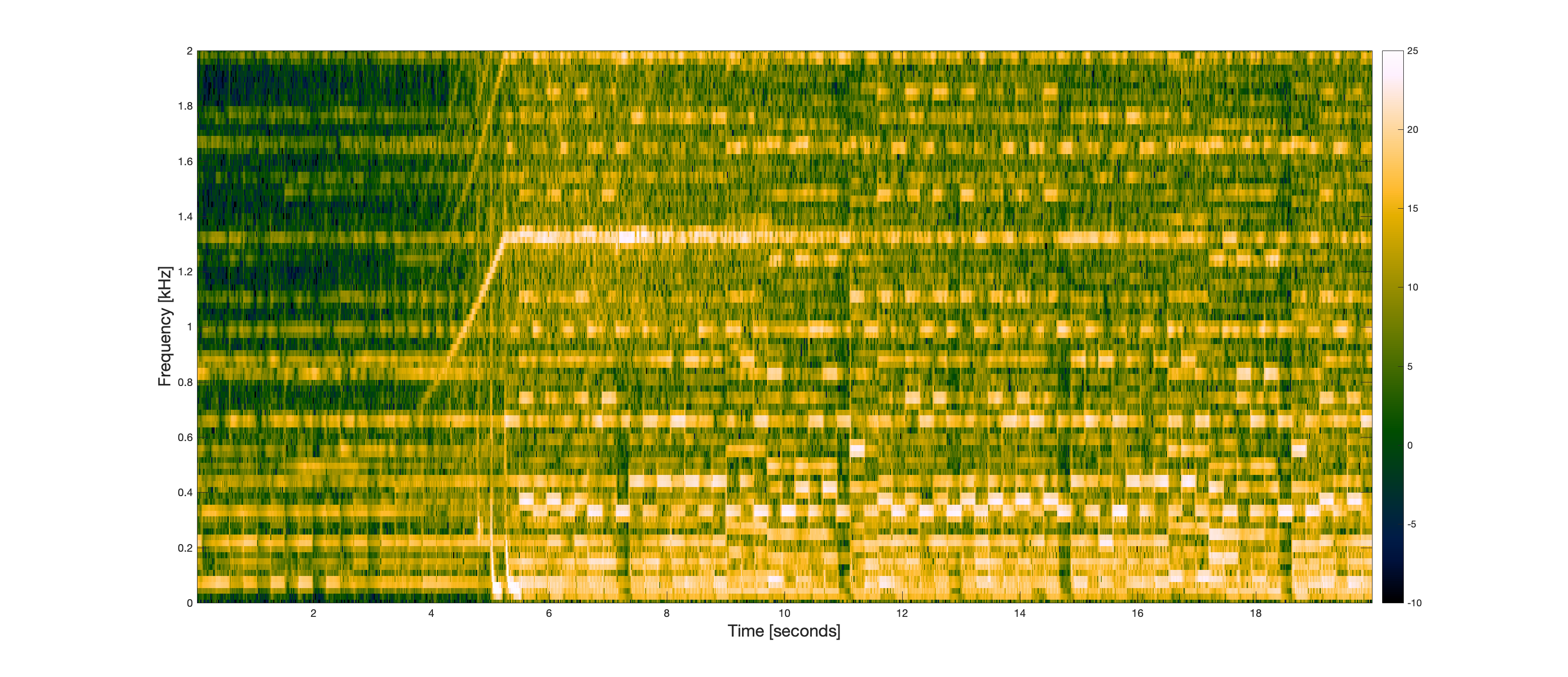
By the way, here is the spectrogram of this segment of the signal. The spectrogram exposes the manner in which signal energy is distributed over time and frequency.

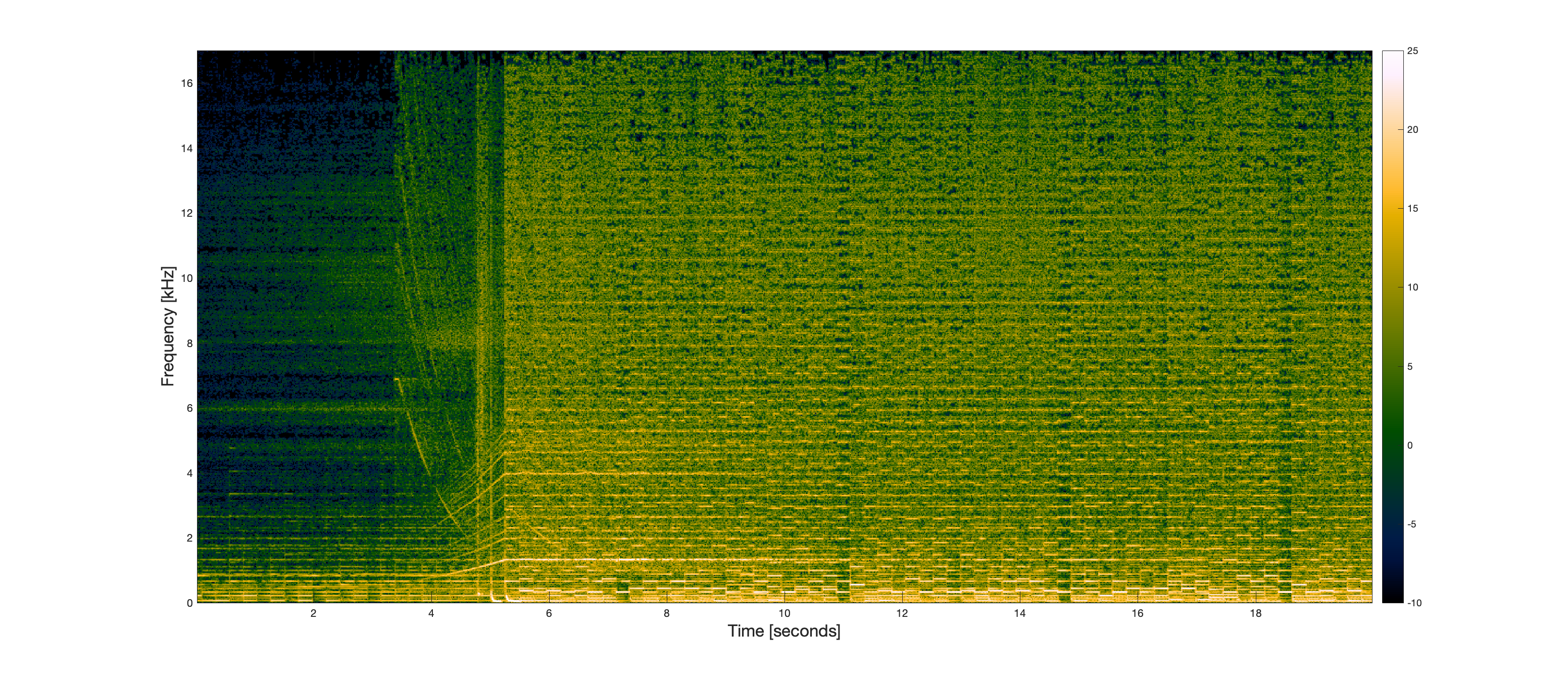
When you listen to the signal, you can hear the structures that can be seen in the spectrogram. You can see the notes more easily by looking at just the first two kilohertz of frequency.

Here are seconds 5 through 12.

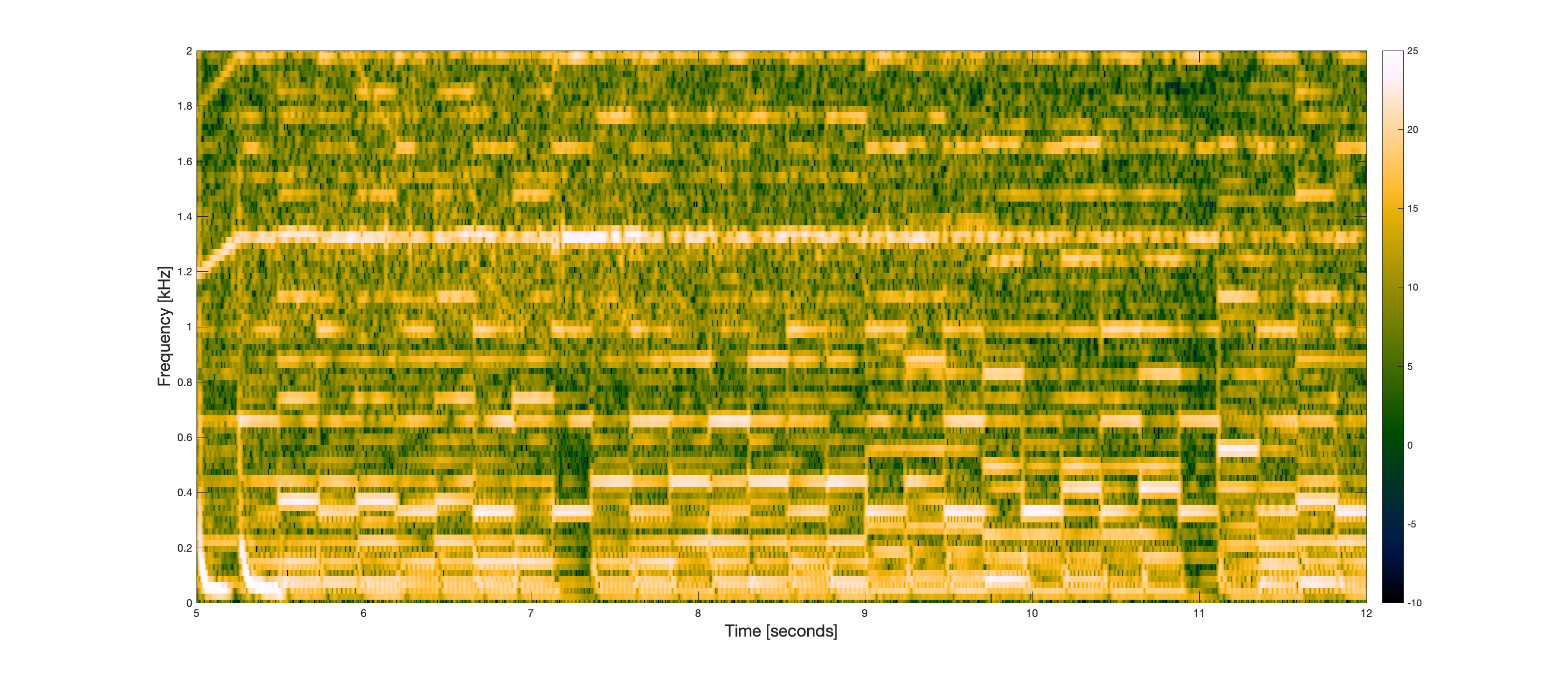
Notice the falling frequency characteristic of the drums at the start of this segment. This can be visualized in the time domain as well.

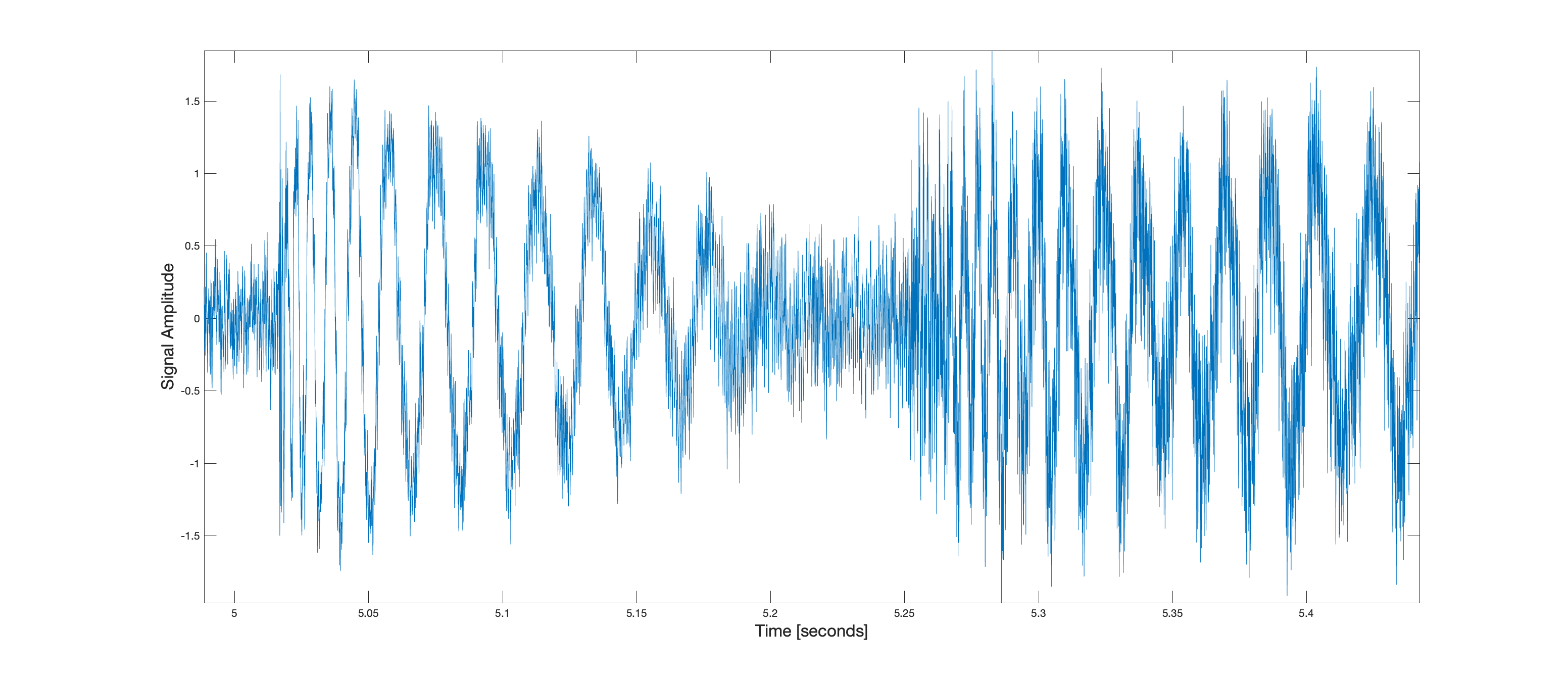
You can see the frequency falling from high to low in the waveform.

3. This video is a signal. Characterize this signal in terms of:

   • Domain (continuous or discrete)

   • Range (continuous or discrete)

   • Dimension (number of independent variables)

   • Channels (number of dependent variables)

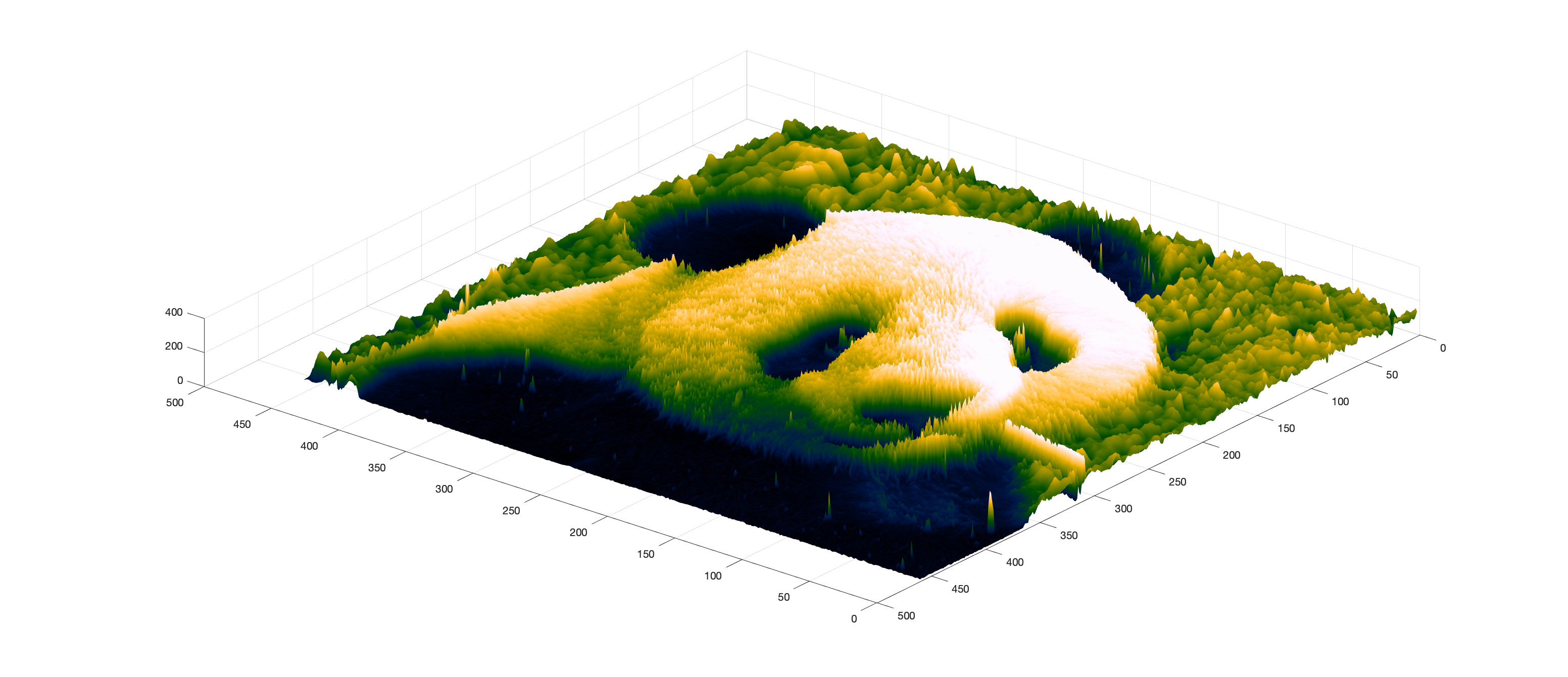
4. The image below is a signal.

Characterize this signal in terms of:

• Domain (continuous or discrete)

• Range (continuous or discrete)

• Dimension (number of independent variables)

• Channels (number of dependent variables)

To illustrate that this picture reall is a function of two independent variables, consider a surface plot of the same image.

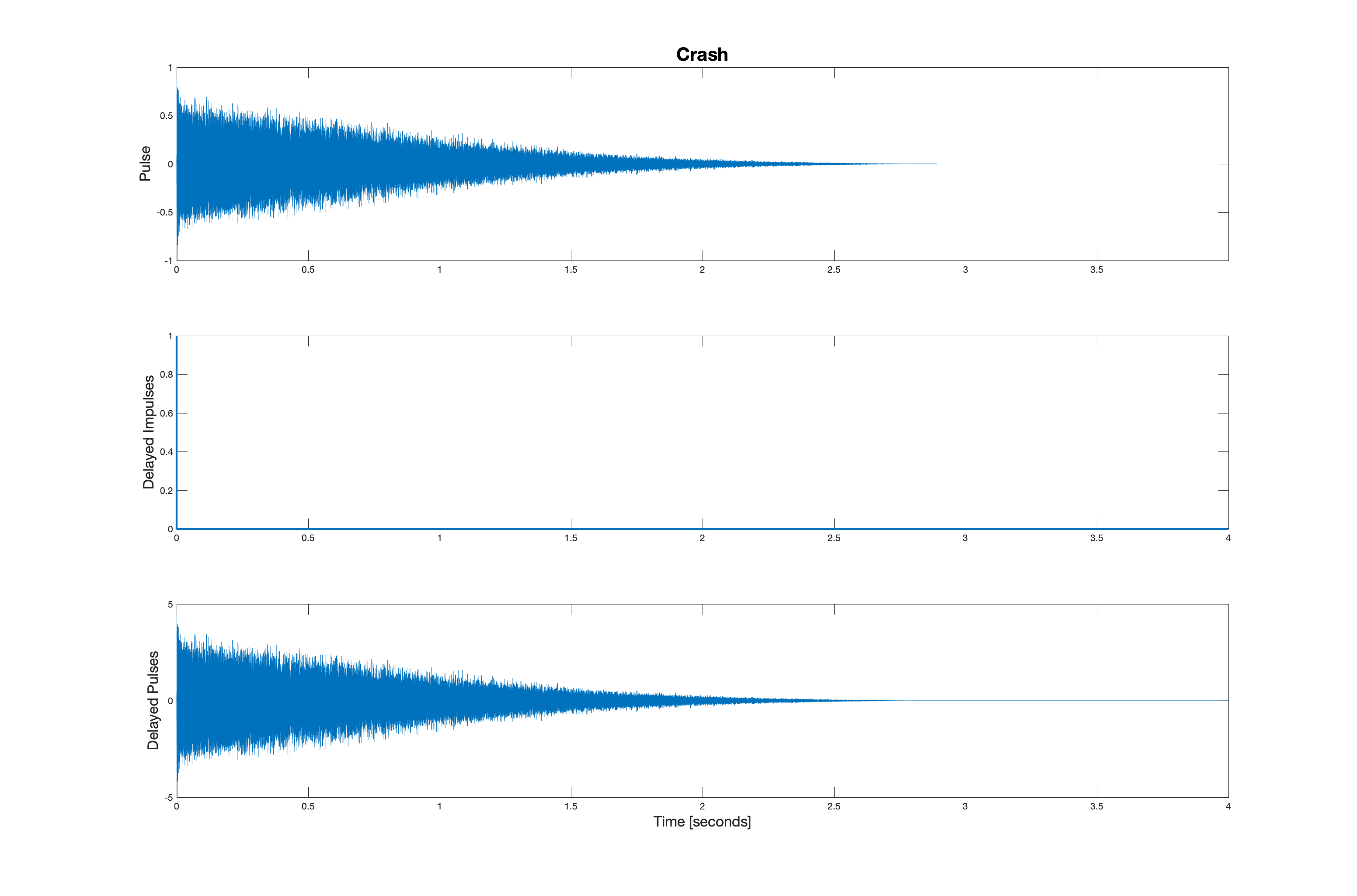
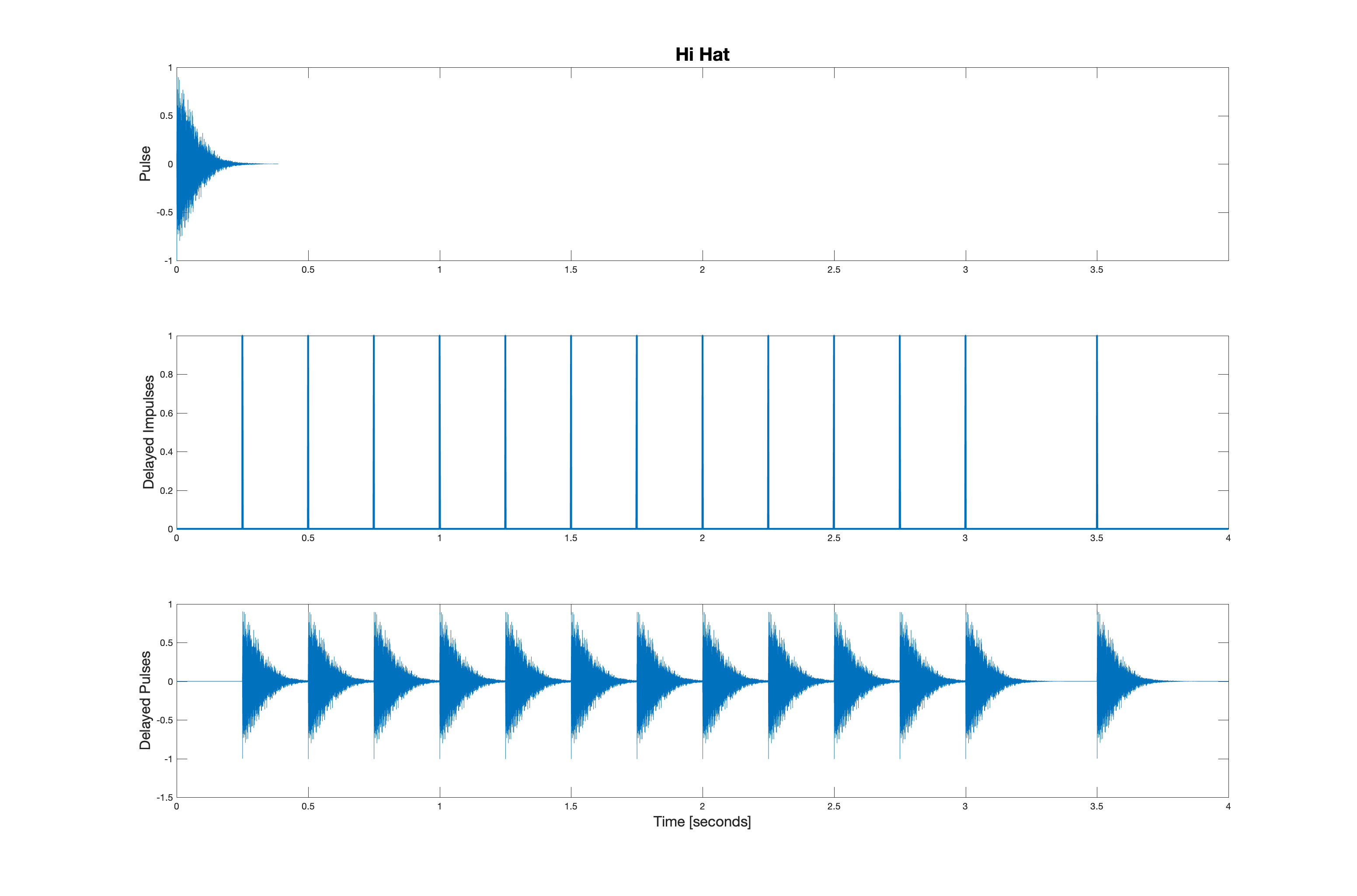
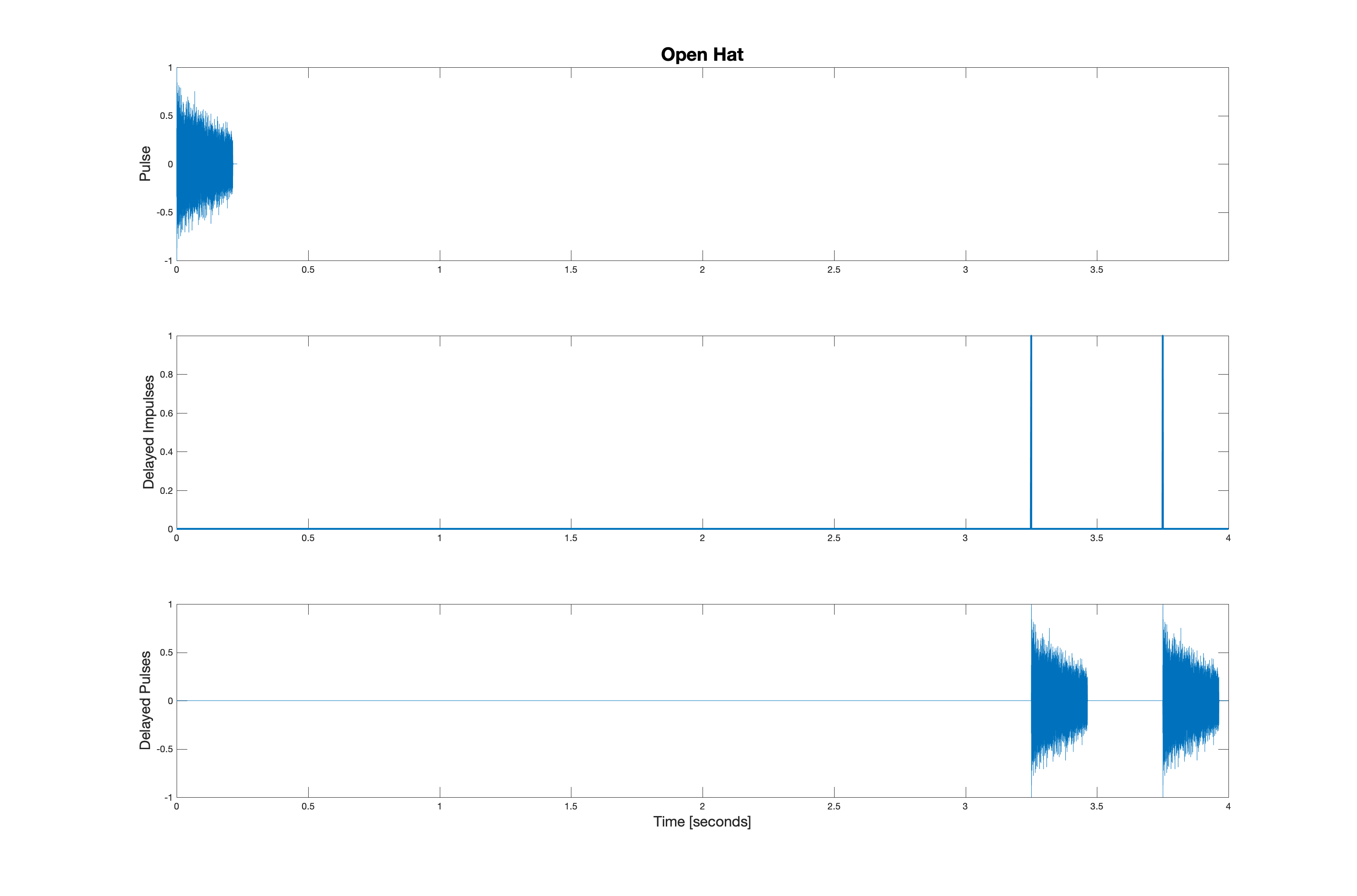
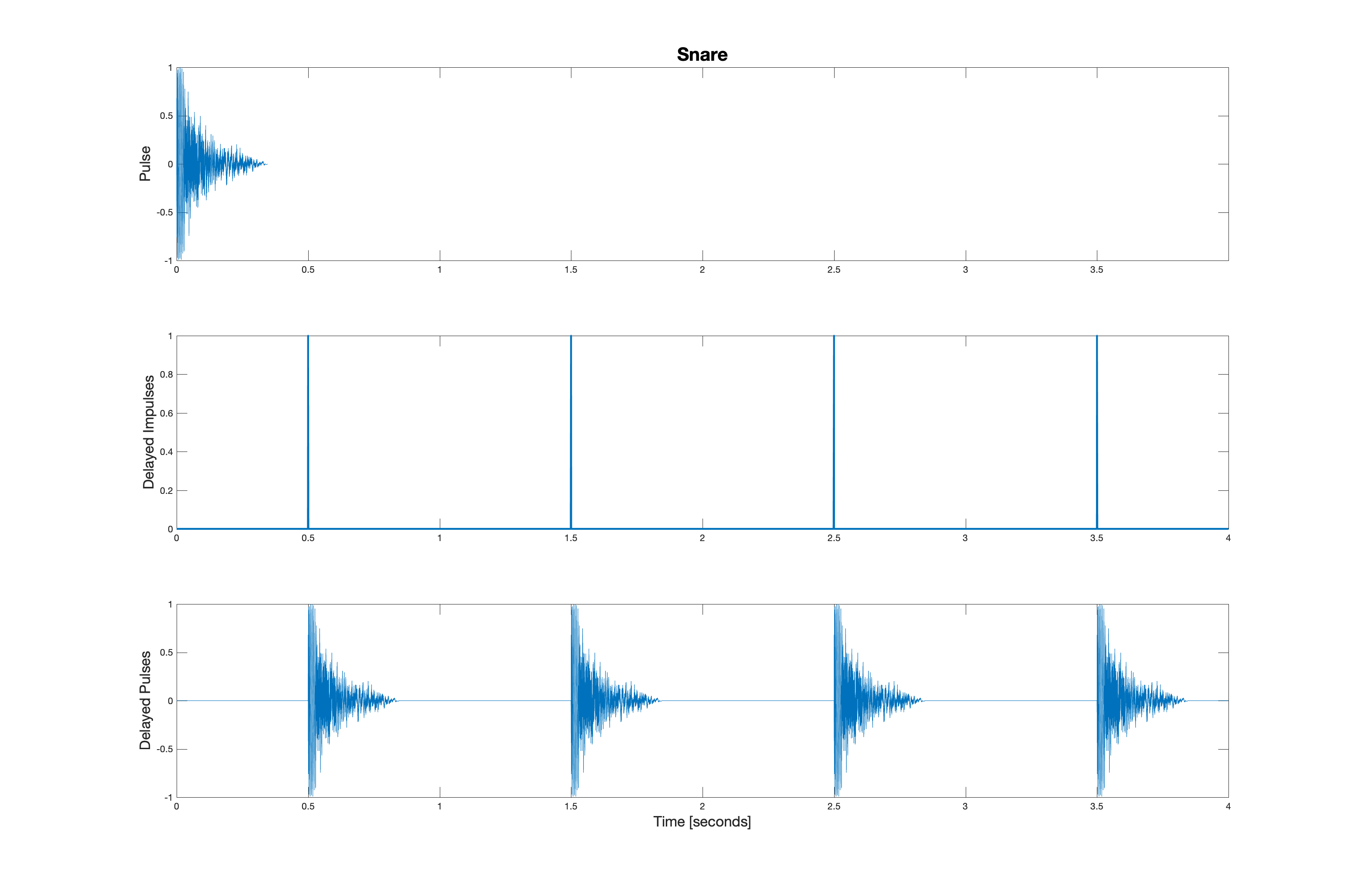
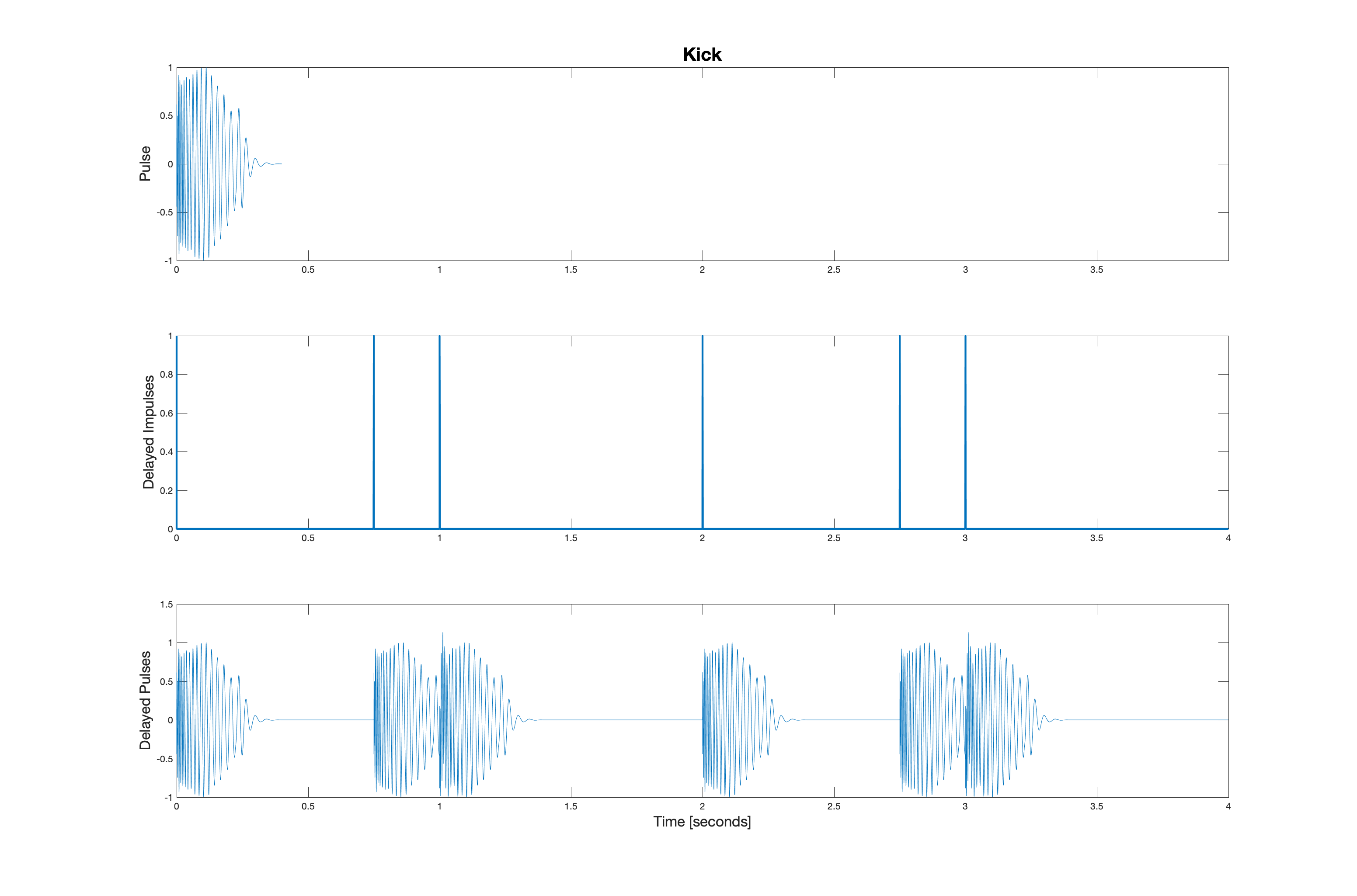
5. Convolution with delayed impulses leads to delayed replicas of a signal. Consider the five audio signals shown below.

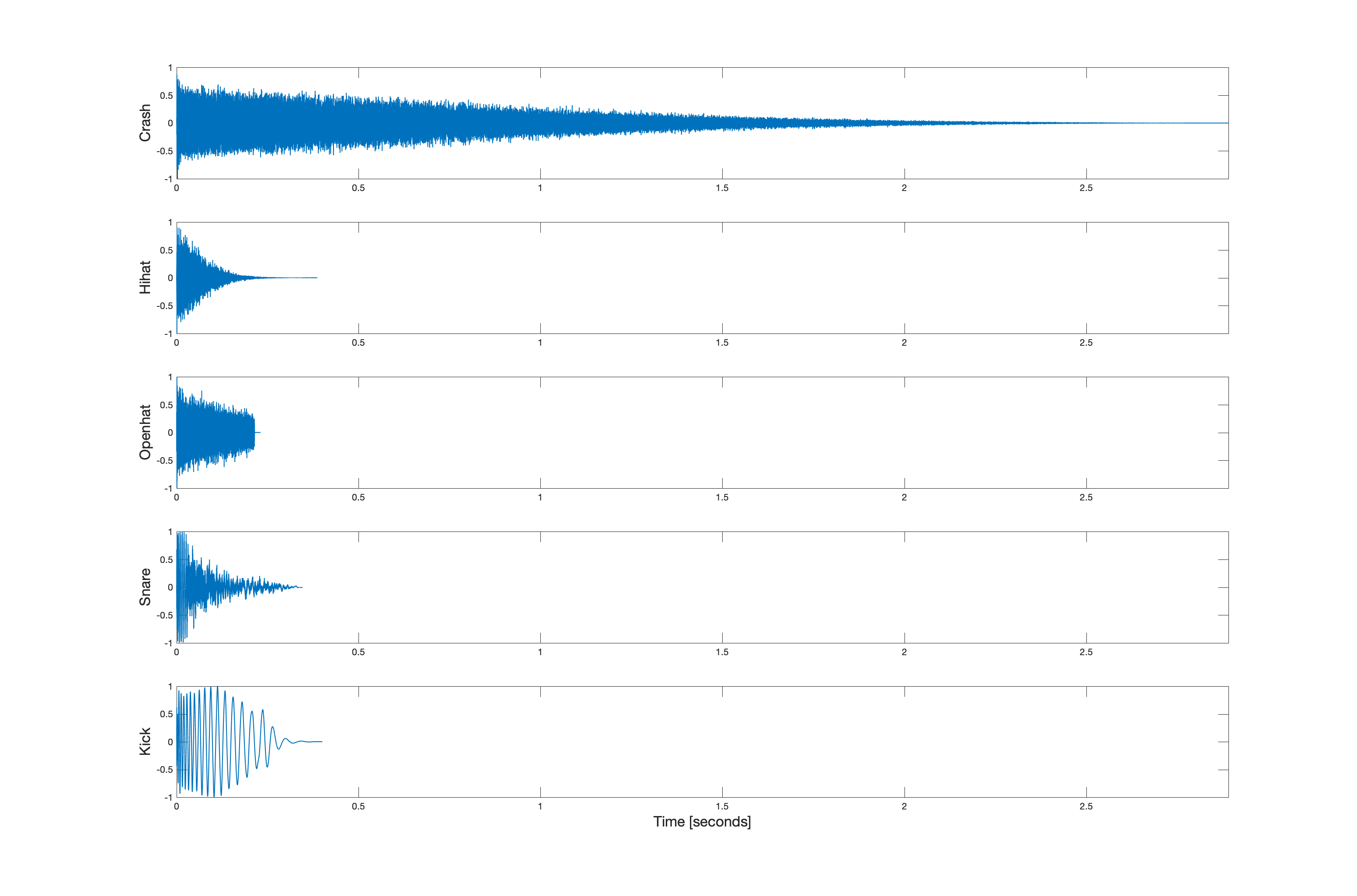
These signals sound like this: crash, hihat, openhat, snare, and kick.

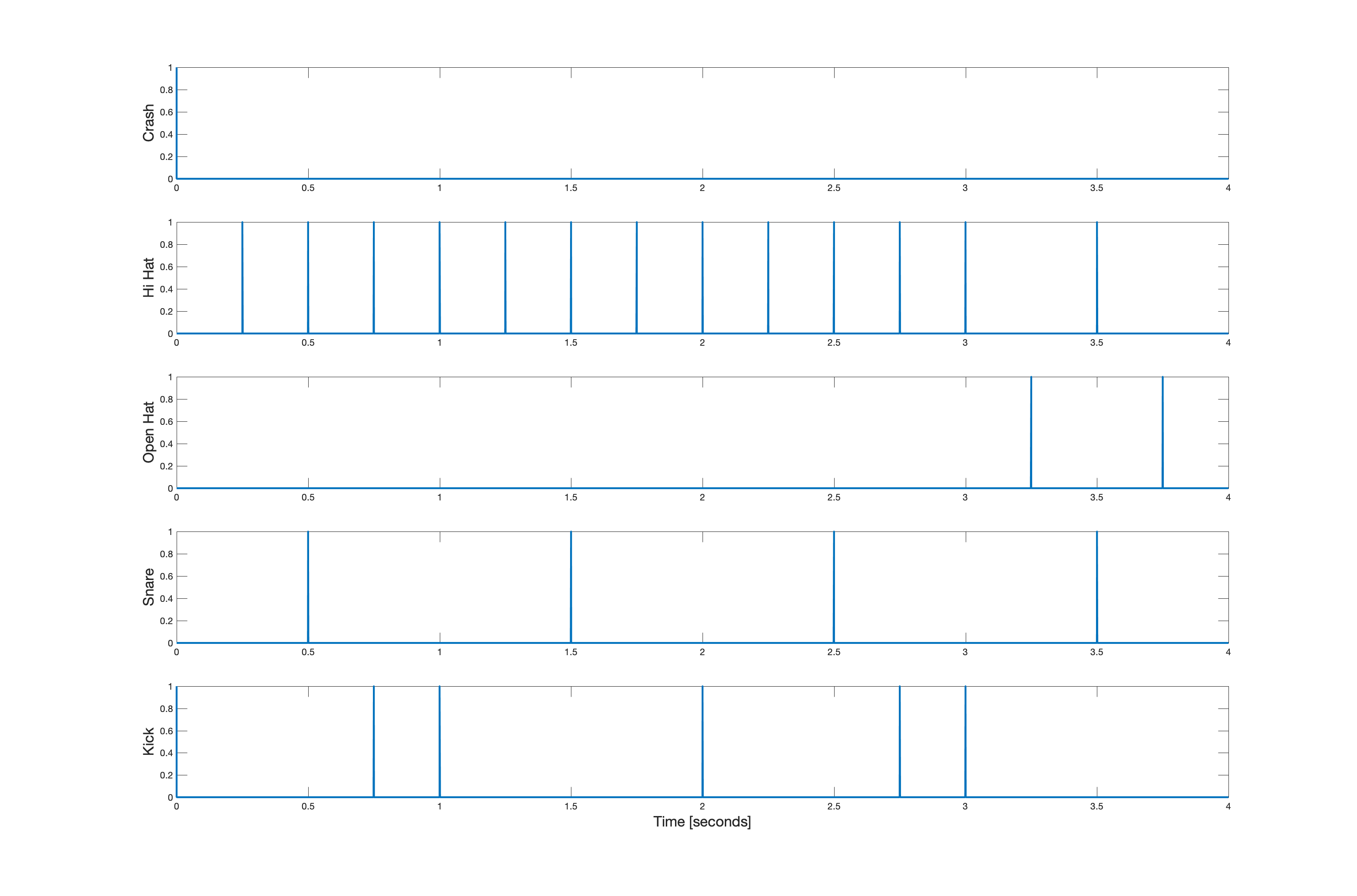
Suppose these five signals are convolved (respectively) with the five impulse patterns shown below.

Let's consider each case separately. First the crash sound. This one is not very interesting because there is only one delta function and it is positioned at the origin $\delta [n]$$\delta[n]$. Convolution of any signal with $\delta [n]$$\delta[n]$ reproduces the original signal.

The other drum kit sounds are a little bit more interesting. They are shown below in order: hi hat, open hat, snare, and kick. Clicking on these images will play the pulse train sound.

This yields the five waveforms shown below. Be sure you see the connection between the location of the impulses and the replicas that result from convolution.

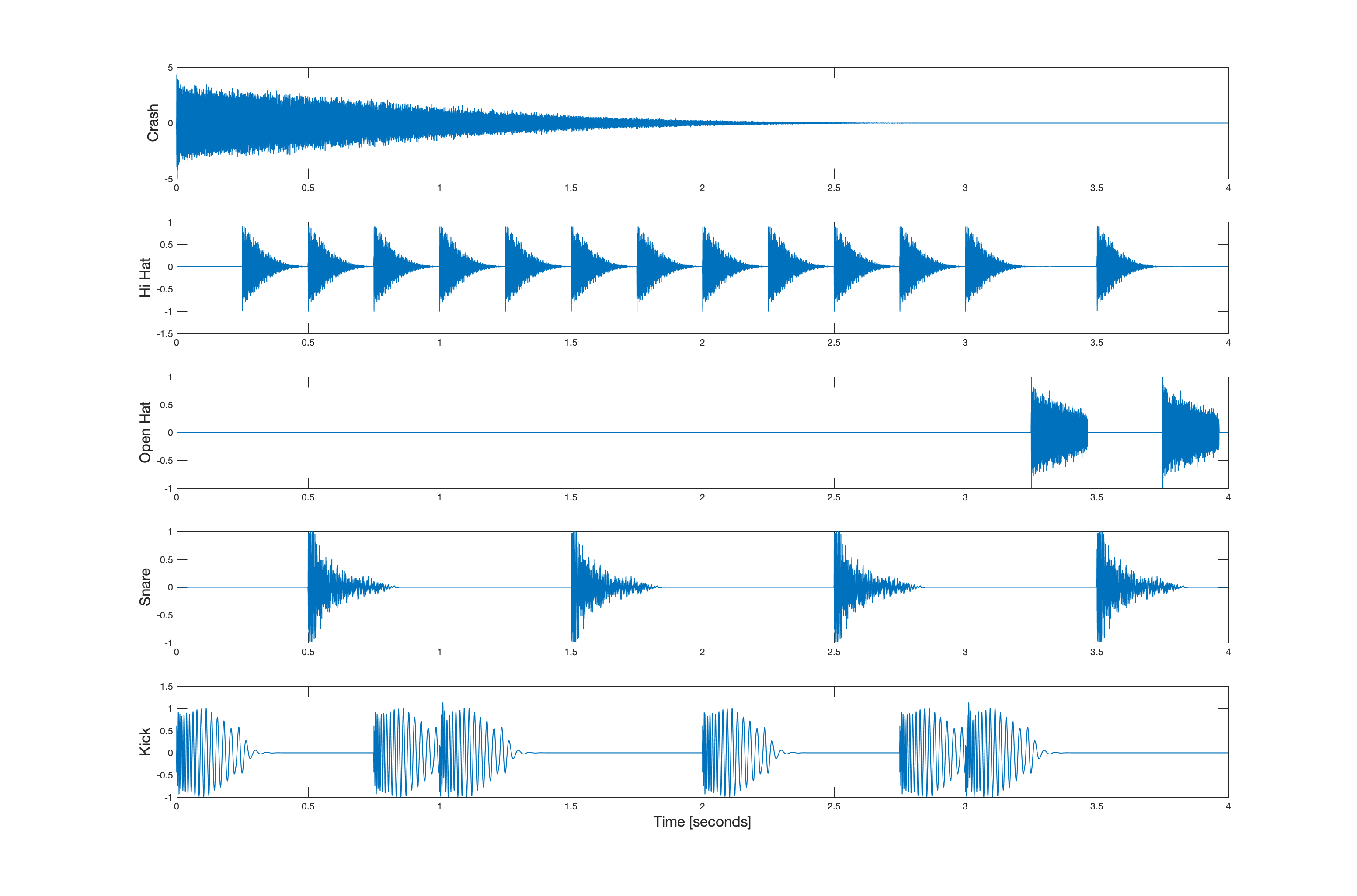
When these five signals are added together, we have the following waveform.

Click here to listen.

6. Sinc function in continuous time.

Question. For the sinc function

find the zeros and the amplitude when $t=0$$t=0$. The zeros of $x(t)$$x(t)$ are values the values of $t$$t$ where $x(t)=0$$x(t)=0$.

Answer. Roughly speaking, a ratio of functions of $t$$t$ such as the sinc function is zero at those values of $t$$t$ where the numerator function is zero, but care must be taken to consider $\frac{0}{0}$$\frac{0}{0}$ cases. The set of candidate zeros occur when the numerator function is zero,

The $\sin$$\sin$ function is zero whenever its argument is an integer multiple of pi,

Solving for $t$$t$ yields the set of candidate zeros

Apparently there is the potential for an infinite number of zeros. However, one the candidate zeros results in a $\frac{0}{0}$$\frac{0}{0}$ condition, and that is the $k=0$$k=0$ case. In this case, the value of the function may be obtained using L'Hopital's Rule, which is

where $f^{\prime }(t),g^{\prime }(t)$$f'(t), g'(t)$ are derivatives of $f(t),g(t)$$f(t), g(t)$, respectively. Applying this rule to the sinc function yields

Therefore, the $k=0$$k=0$ case is not a zero. Rather the sinc function takes on the value $W$$W$ when $t=0$$t=0$. In summary, we have learned that:

• The sinc function $\frac{\sin (\pi Wt)}{\pi t}$$\frac{\sin(\pi W t)}{\pi t}$ has a countably infinite number of zeros. With the exception of the $k=0$$k=0$ case, the zeros are preiodically repeating at $t=\frac{k}{W}$$t=\frac{k}{W}$ where $k=\pm 1,\pm 2,\pm 3,\cdots$$k=\pm 1, \pm 2, \pm 3, \cdots$.

• When $t=k=0$$t=k=0$, the sinc function takes on the value

Here is a plot of the sinc function for $W=\frac{1}{2},1,2$$W = \frac{1}{2}, 1, 2$. Notice how the peak amplitude at $t=0$$t=0$ increases with $W$$W$. Notice that the zeros (red dots) occur periodically at multiples of $\frac{1}{W}$$\frac{1}{W}$. Notice that the density of zeros increases with $W$$W$.

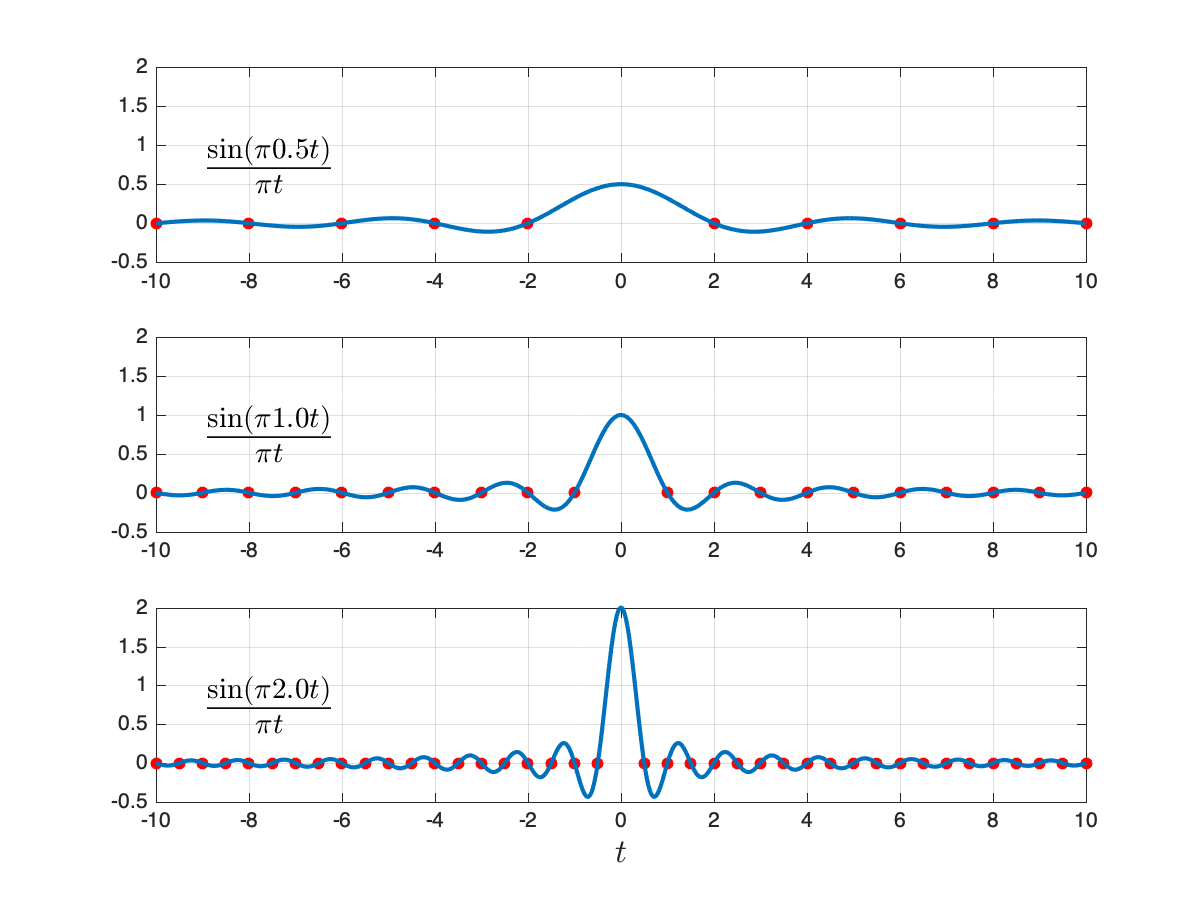
Here is another plot comparing sinc functions for 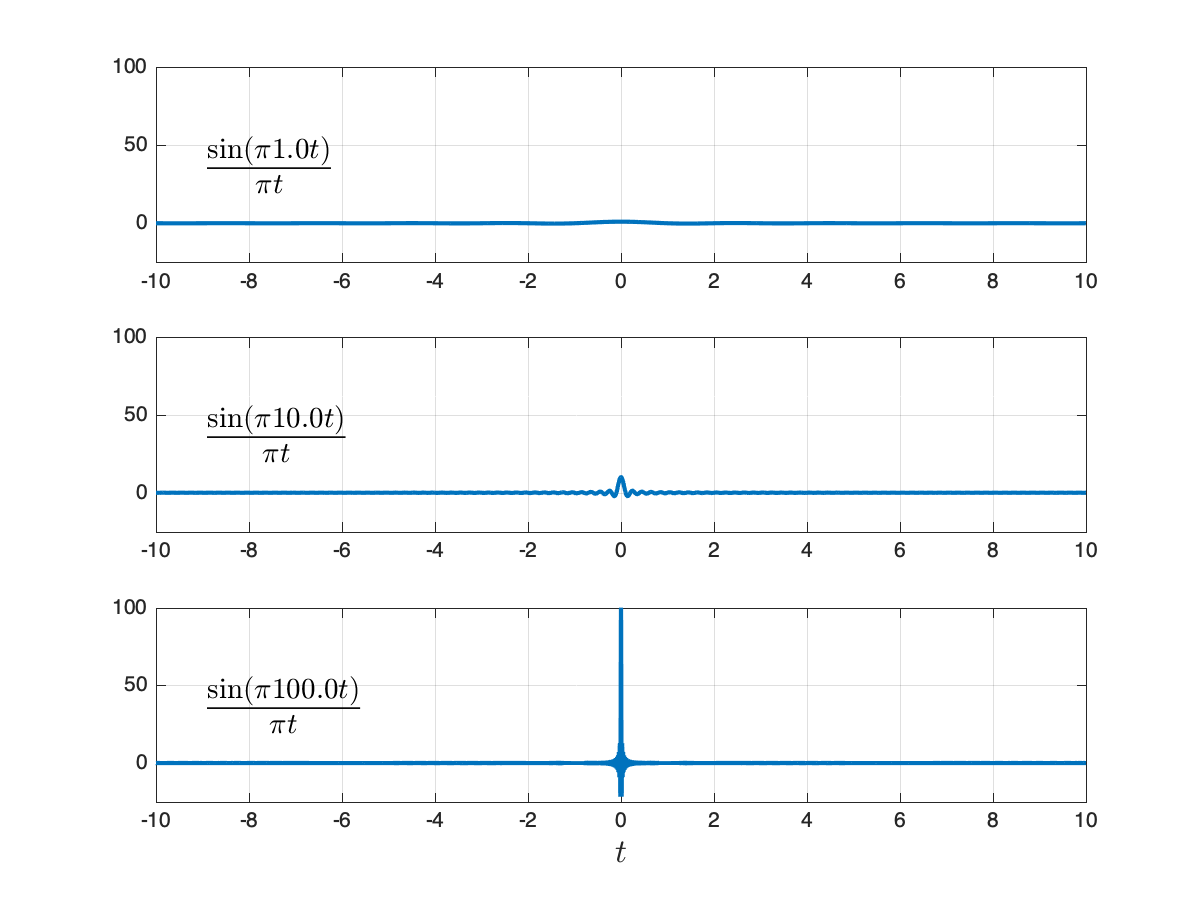$W=1,10,100$$W=1, 10, 100$.

7. Sinc function in continuous time.

Question. For the sinc function

find the zeros and the amplitude when $t=0$$t=0$. The zeros of $x(t)$$x(t)$ are the values of $t$$t$ where $x(t)=0$$x(t)=0$.

Answer. The zero crossings occur at $t=\pm 1,\pm 2,\cdots$$t=\pm 1, \pm 2, \cdots$, and

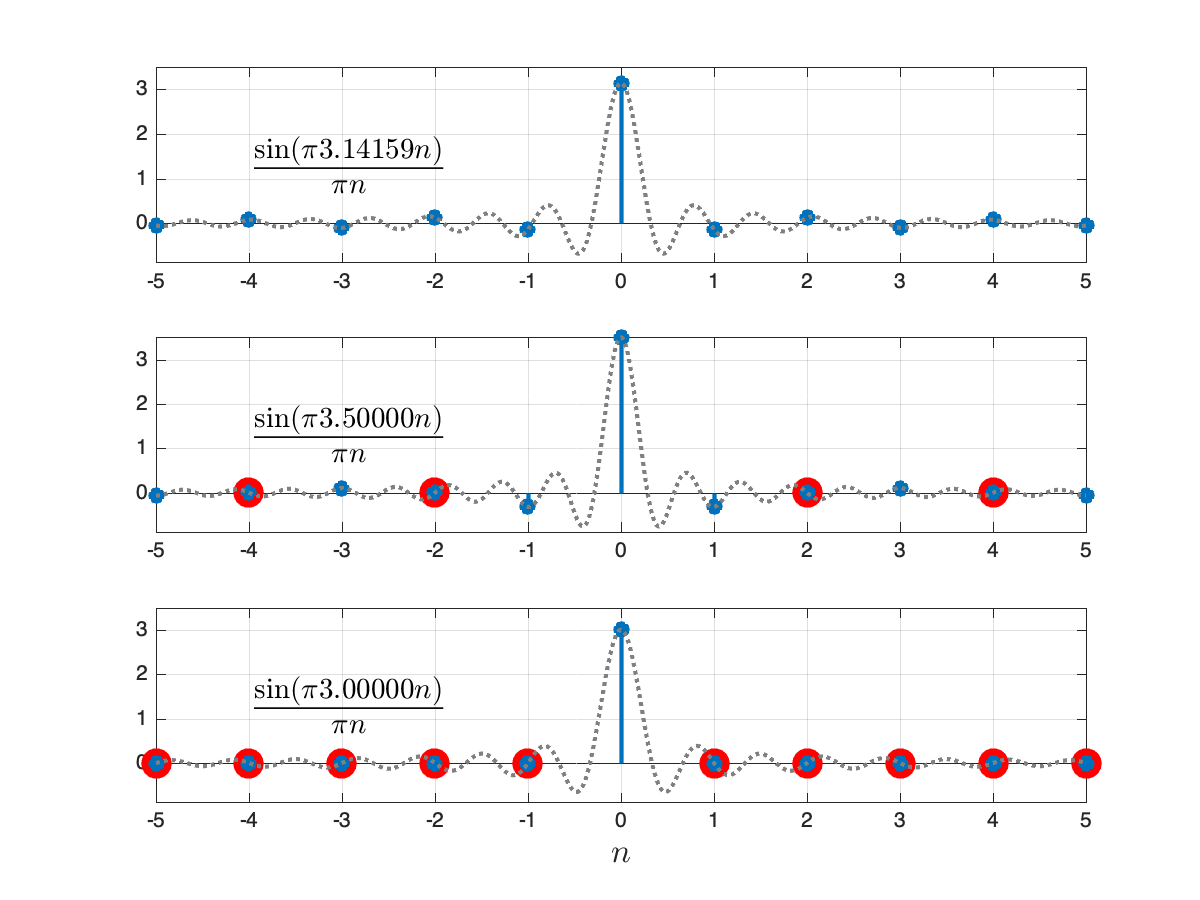
8. Sinc function in discrete time.

Question. For the sinc function

find the zeros and the amplitude when $n=0$$n=0$. The zeros of $x[n]$$x[n]$ are the values of $n$$n$ where $x[n]=0$$x[n] = 0$.

Answer. Using the reasoning from above, the amplitude when $n=0$$n=0$ is $M$$M$. The zeros occur when

Canceling $\pi$$\pi$ on both sides leaves

This equation must be satisfied for integers $n$$n$ and $k$$k$. Remember that the discrete time signal $x[n]$$x[n]$ is only defined for integer $n$$n$. Hence, there are several cases to consider.

• $M$$M$ is irrational. In this case, $Mn$$Mn$ is irrational for all $n$$n$. There are no values of $n$$n$ for which $x[n]=0$$x[n] = 0$.

• $M$$M$ is rational. Suppose $M=\frac{P}{Q}$$M = \frac{P}{Q}$, where $P$$P$ and $Q$$Q$ are co-prime. Then $Mn=Pn/Q$$Mn = Pn/Q$ is an integer when $n=iQ$$n=iQ$ for integer $i$$i$. In this case, the zeros occur at $n=\pm Q,\pm 2Q,\pm 3Q,\cdots$$n=\pm Q, \pm 2Q, \pm 3Q, \cdots$.

• $M$$M$ is an integer. In this case, $Mn$$Mn$ is an integer for all integer $n$$n$. Therefore, the zeros occur at $n=\pm 1,\pm 2,\pm 3,\cdots$$n= \pm 1, \pm 2, \pm 3, \cdots$. (The integer case may also be viwed as the rational case with $Q=1$$Q=1$.)

The plot below illustrates these there cases for $M=\pi ,3.5,3$$M=\pi, 3.5, 3$. The red circles highlight the zeros. When $M=\pi$$M=\pi$, there are no zeros. When $M=\frac{7}{2}=3.5$$M=\frac{7}{2}=3.5$, the zeros occur at multiples of $2$$2$. When $M=3$$M=3$, $n=\pm 1,\pm 2,\pm 3,\cdots$$n=\pm 1, \pm 2, \pm 3, \cdots$ are all zeros.

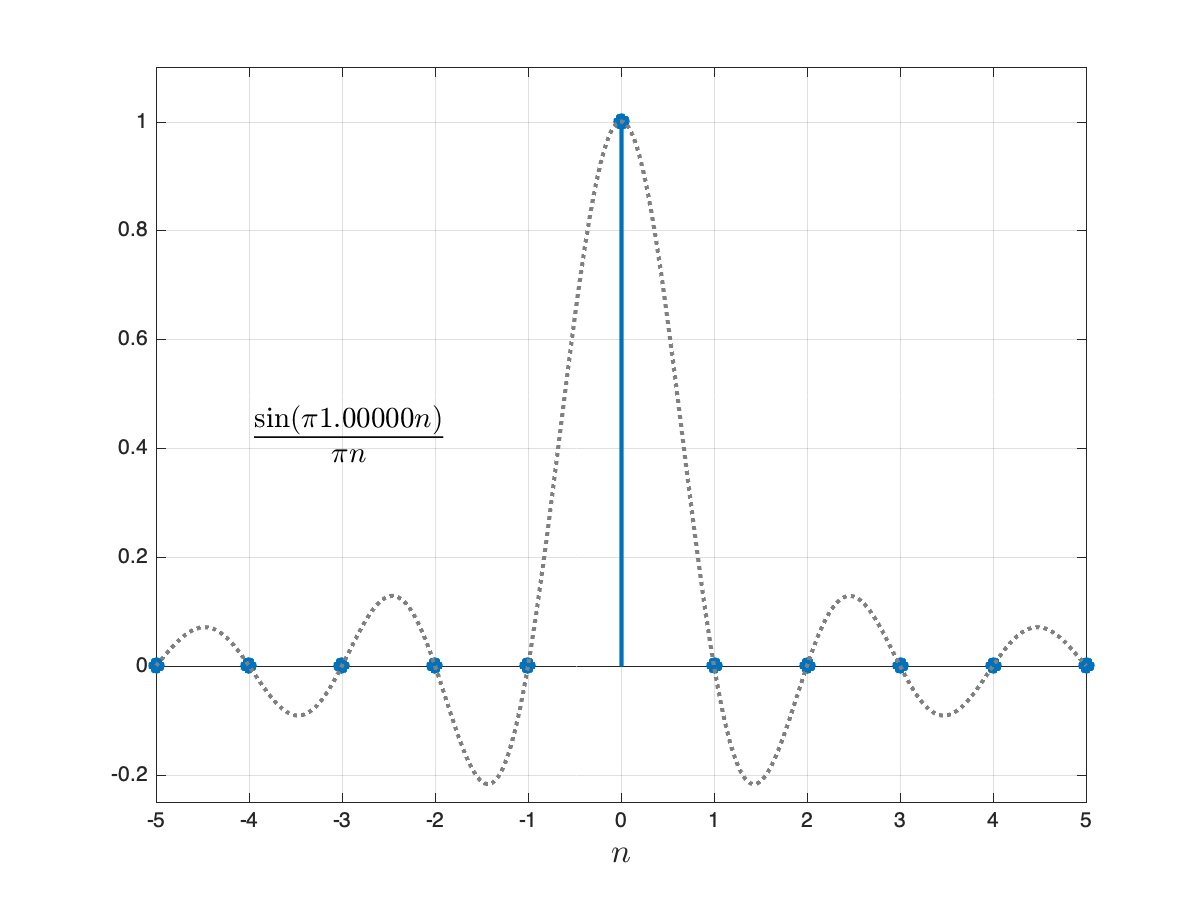
As a special case of the above for $M=1$$M=1$, note that

This is illustrated in the figure below.

9. Periodic sinc function.

Question. For the periodic sinc function

find the zeros and the amplitude at points where $X(f)=\frac{0}{0}$$X(f) = \frac{0}{0}$. Assume that $N$$N$ is an integer.

Answer. First observe that $X(f)$$X(f)$ is periodic with period of $1$$1$. In other words, $X(f+k)=X(f)$$X(f+k) = X(f)$ for all integers $k$$k$.

The numerator function $\sin (\pi Nf)$$\sin(\pi N f)$ zeros will occur when

The demoninator function $\sin (\pi f)$$\sin(\pi f)$ zeros will occur when

The $X(f)=\frac{0}{0}$$X(f) = \frac{0}{0}$ condition occurs when both $Nf$$Nf$ and $f$$f$ are integers, which occurs whenever $f$$f$ is an integer. The value of the $X(f)$$X(f)$ for integer $f$$f$ may be obtained using L'Hopital's Rule,

$X(f)$$X(f)$ takes on the same valueu $N$$N$ for all integers $f$$f$.

The set of candidate zeros for $X(f)$$X(f)$ are $Nf=k$$Nf=k$ or $f=k/N$$f=k/N$ for integer $k$$k$. Since we know that $X(f)=N$$X(f)=N$ when $f$$f$ is an integer, we find that there are $N-1$$N-1$ zeros of $X(f)$$X(f)$ in every period. In the base period $0\le f<1$$0\leq f < 1$, the zeros occur at $f=\frac{1}{N},\frac{2}{N},\cdots ,\frac{N-1}{N}$$f=\frac{1}{N}, \frac{2}{N}, \cdots, \frac{N-1}{N}$. The zeros in the $m^{\text{th}}$$m^\text{th}$ period occur at $f=\frac{1}{N}+m,\frac{2}{N}+m,\cdots ,\frac{N-1}{N}+m$$f=\frac{1}{N}+m, \frac{2}{N}+m, \cdots, \frac{N-1}{N}+m$ , where $m$$m$ is any integer. For reference, two periods $-1\le f<1$$-1 \leq f < 1$ of the periodic sinc function for $N=5,9,21$$N=5, 9, 21$ are shown in the figure below.

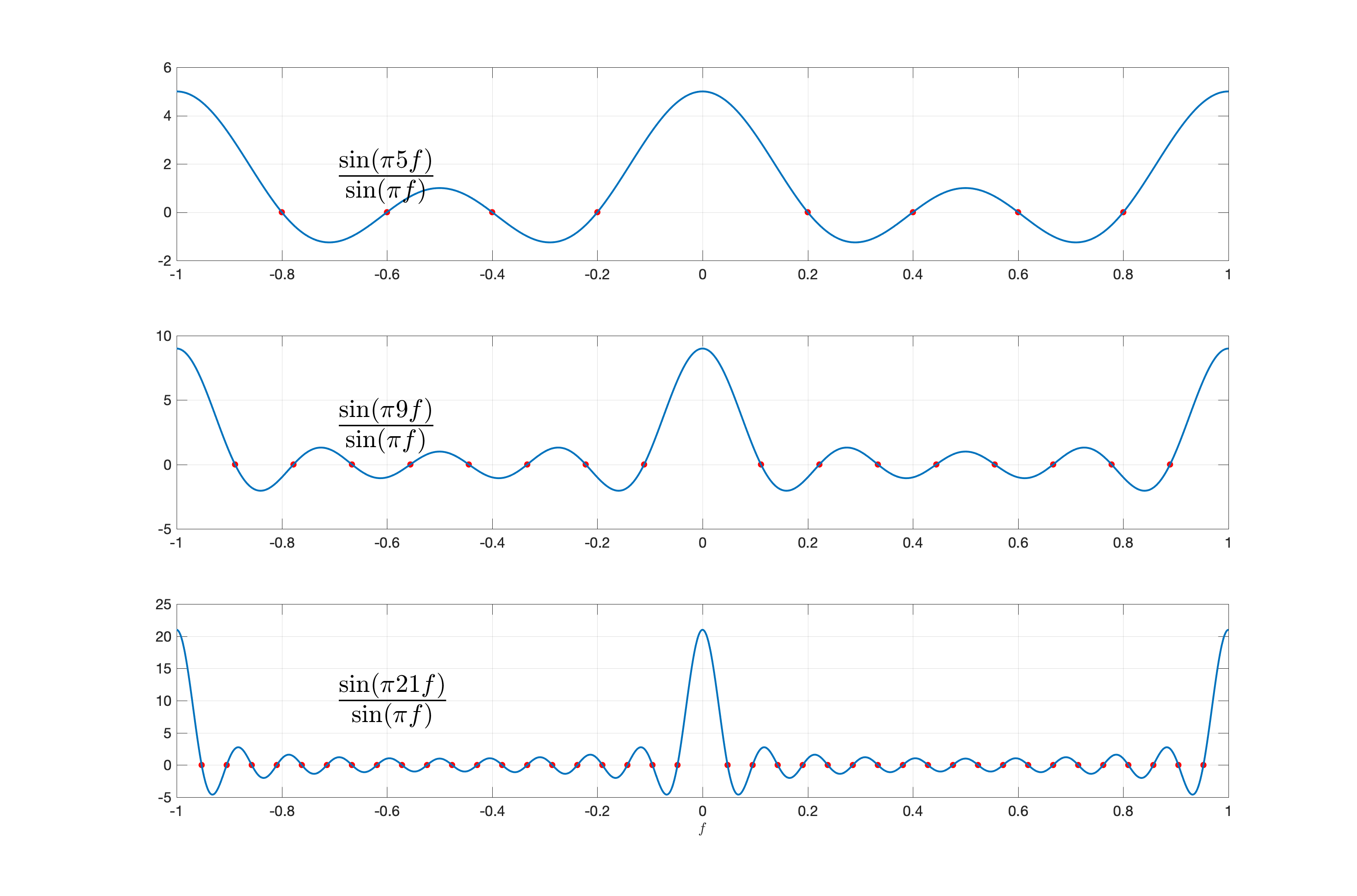
10. Complex exponential signals.

The figure below shows eight different complex exponential signals of the form $a^{n}u[n]$$a^n u[n]$. Match up the signals with the $a$$a$ values in the complex plane shown below.

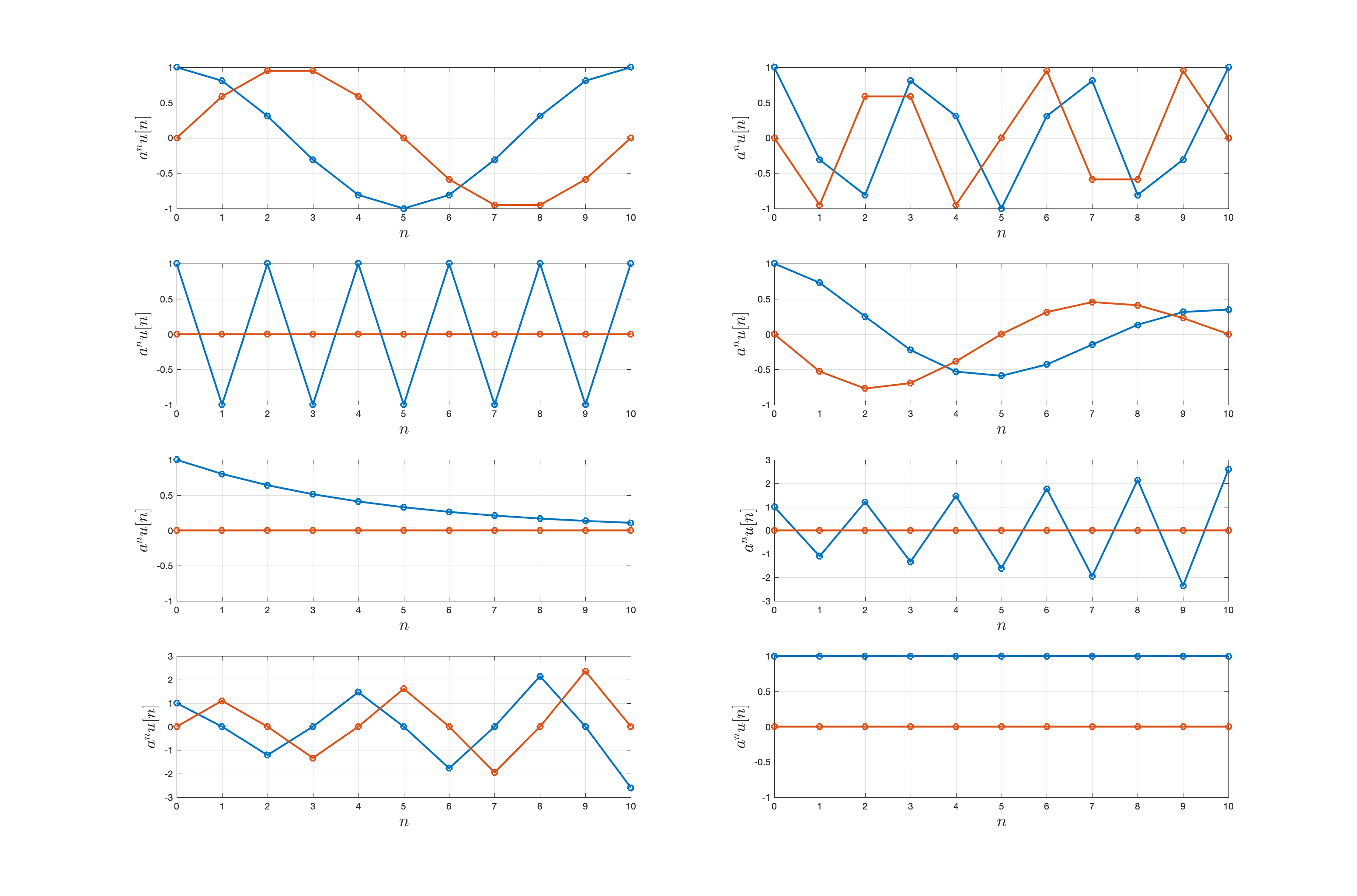
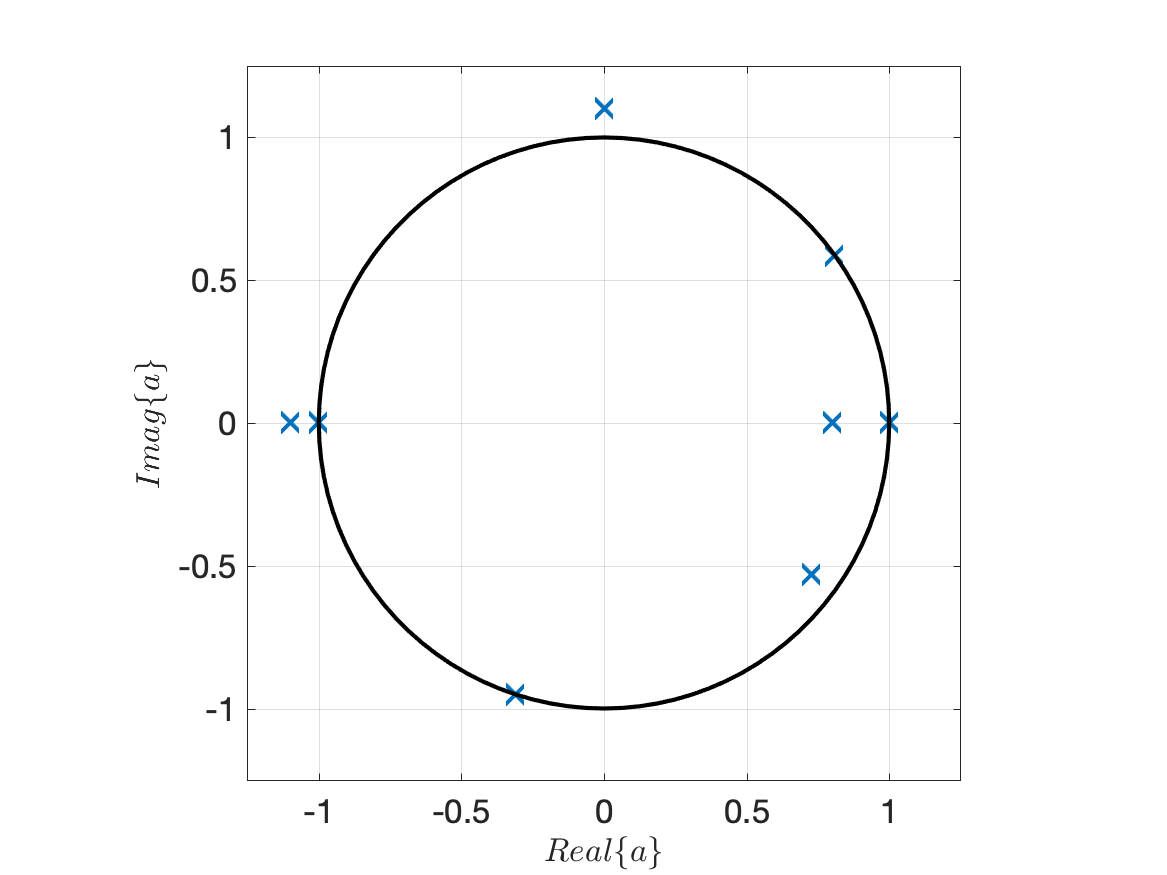
11. Complex exponential signals.

Consider the complex exponential signal $x[n]=e^{j2\pi 38.9n}$$x[n] = e^{j2\pi 38.9 n}$.

• What is its frequency?

• What are the units of frequency in discrete-time?

• What is the alias of this frequency in the interval $0\le f<1$$0 \leq f < 1$?

• What is the alias of this frequency in the interval $-\frac{1}{2}\le f<\frac{1}{2}$$-\frac{1}{2} \leq f < \frac{1}{2}$?

12. Sketch a picture of the following types of signals.

• Causal

• Anti-causal

• Non-causal

• Non-anti-causal

• Causal left-sided

• Non-causal left-sided

• Anti-causal right-sided

• Non-anti-causal right-sided

• Causal finite

• Non-causal finite

• Doubly infinite (two-sided)

13. Sifting property of Kronecker delta.

Question.

Answer.

14. Convolution property of Kronecker delta.

Question.

Answer.