DTFT Symmetries

The symmetry properties of the DTFT are clarified by considering a special four-way decomposition of sequences and functions. The DTFT is a mapping between the four parts of a sequence-function pair.

Even and odd parts of sequences and functions

The even and odd parts of a sequence $x[n]$ may be computed as

For a function $X(f)$ the even and odd parts may be computed as

Similarly, the real and imainary parts of sequences and functions may be computed as

Four-way decomposition of sequences and functions

Any sequence $x[n]$ or function $X(f)$ admits a four-way decomposition into its real-even, imaginary-even, real-odd, and imaginary-odd parts,

The components in the decomposition can be computed by composing the even, odd, real, and imaginary transformations given above. These may be summarized using the following transformations,

The $(u,v)^\text{th}$ element of the matrix is given by $\Re\{j^{uv}\} + \Im\{j^{uv}\}$, where $u,v \in \{0,1,2,3\}$.

It can be shown (in the homework) that the DTFT transforms the four components of $x[n]$ to the four components of $X(f)$ without mixing the components together. The mapping is given in the figure below.

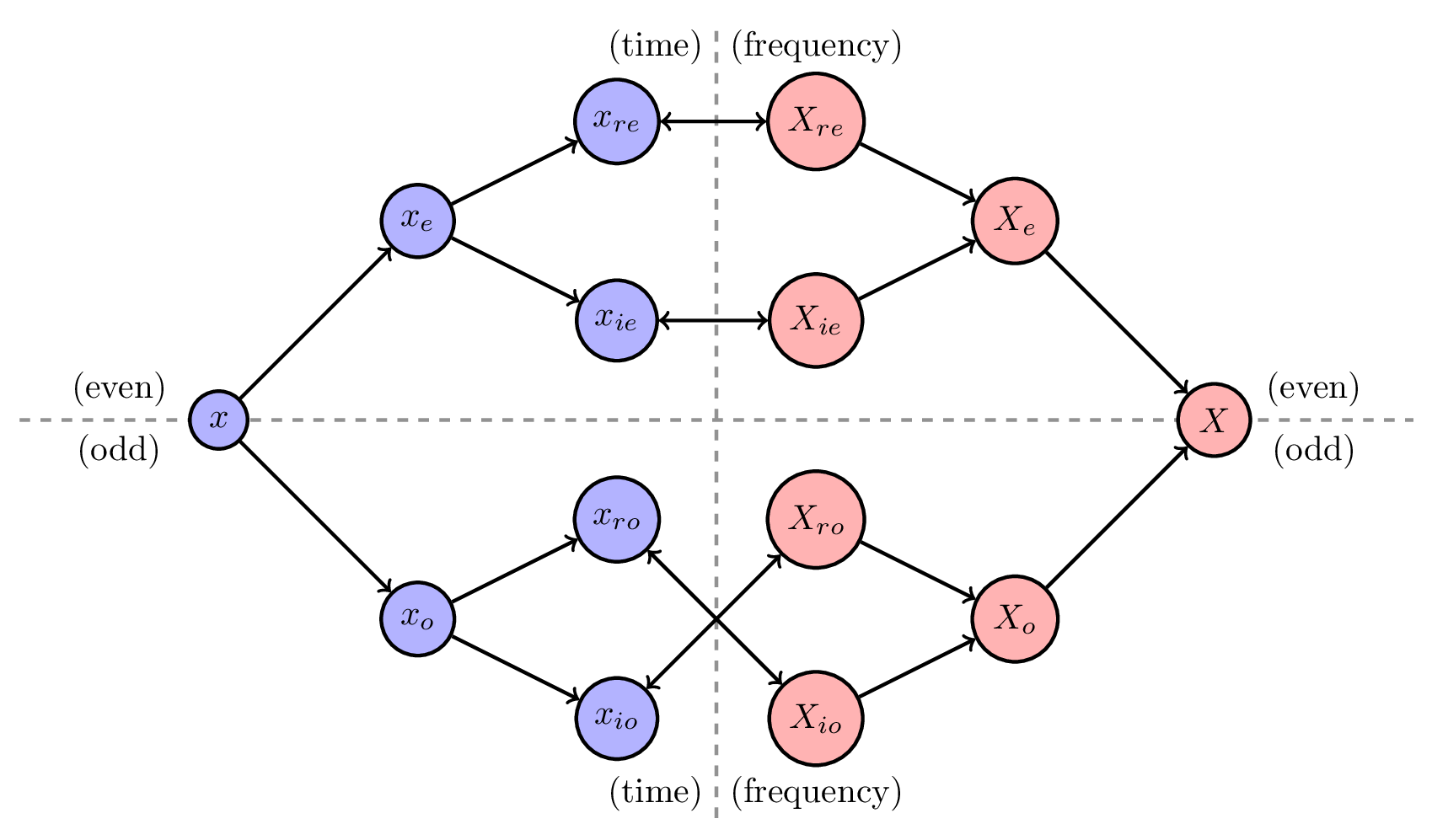
As shown in this diagram, the DTFT transforms a real-even sequence $x_{re}[n]$ to a real-even function $X_{re}(f)$. The DTFT transforms an imaginary-even sequence $x_{ie}[n]$ to an imaginary-even function $X_{ie}(f)$. Other brances in the symmetry diagram describe the DTFT mapping for real-odd and imaginary-odd sequences.

To show how the symmetry diagram may be used, consider the case in which $x[n]$ is a real valued sequence. Therefore, it only has two non-zero components in its four-way decomposition,

The symmetry diagram below is redrawn with only these two components highlighted.

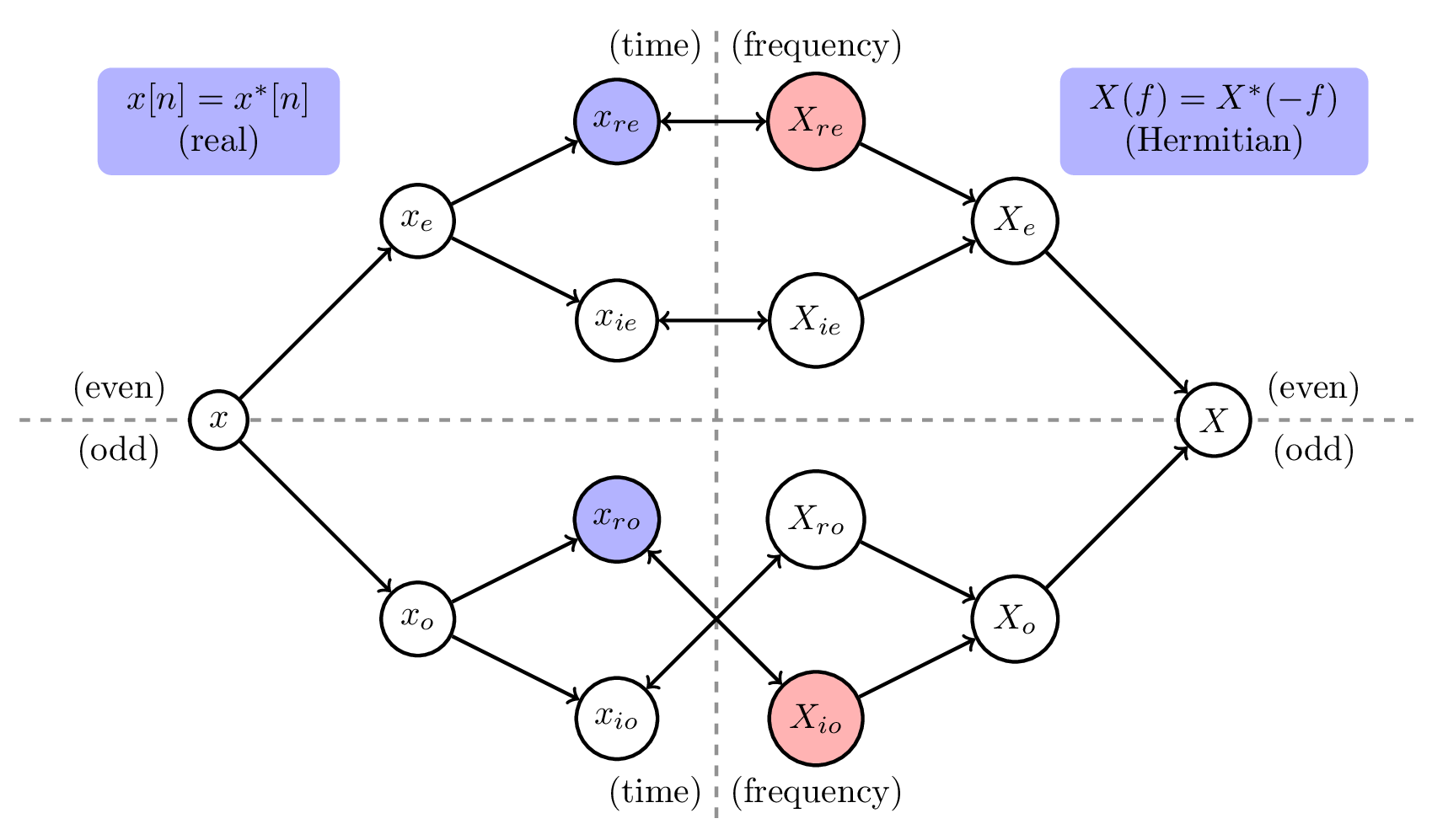
Following the arrows in the diagram shows that $X(f)$, the DTFT of $x[n]$, has only two nonzero components: $X_{re}(f)$ and $X_{io}(f)$. Thus, the real part of the DTFT $X(f)$ of a real sequence $x[n]$ has even symmetry and the imaginary part has odd symmetry. That pair of relations can be summarized in the single statement,

and is referred to as Hermetian symmetry. It can be shown (in the homework) that the magnitude and phase of Hermetian $X(f)$ are, respectively, even and odd functions.

In the general case where $x[n]$ is a complex-valued sequence, no special symmetries need be present in $X(f)$.

When symmetries exist, there is a kind of data compression that is often exploited. For example, when $X(f)$ has Hermetian symmetry, the value of $X(f)$ at negative frequencies $-\frac{1}{2} < f <0$ are redundant. They can be reconstructed from $X(f)$ at positive frequencies $0 < f < \frac{1}{2}$. Therefore, DTFTs of real sequenes are often only plotted for $0 \leq f \leq \frac{1}{2}$, and the negative frequency part is thought of as an appropriately mirrored version of the positive frequency part.

Engineers should get used to immediately looking for symmetries in spectral (DTFT) plots. This can help the engineer understand the type of data being presented or can be used as a means to find bugs in a system implementation.

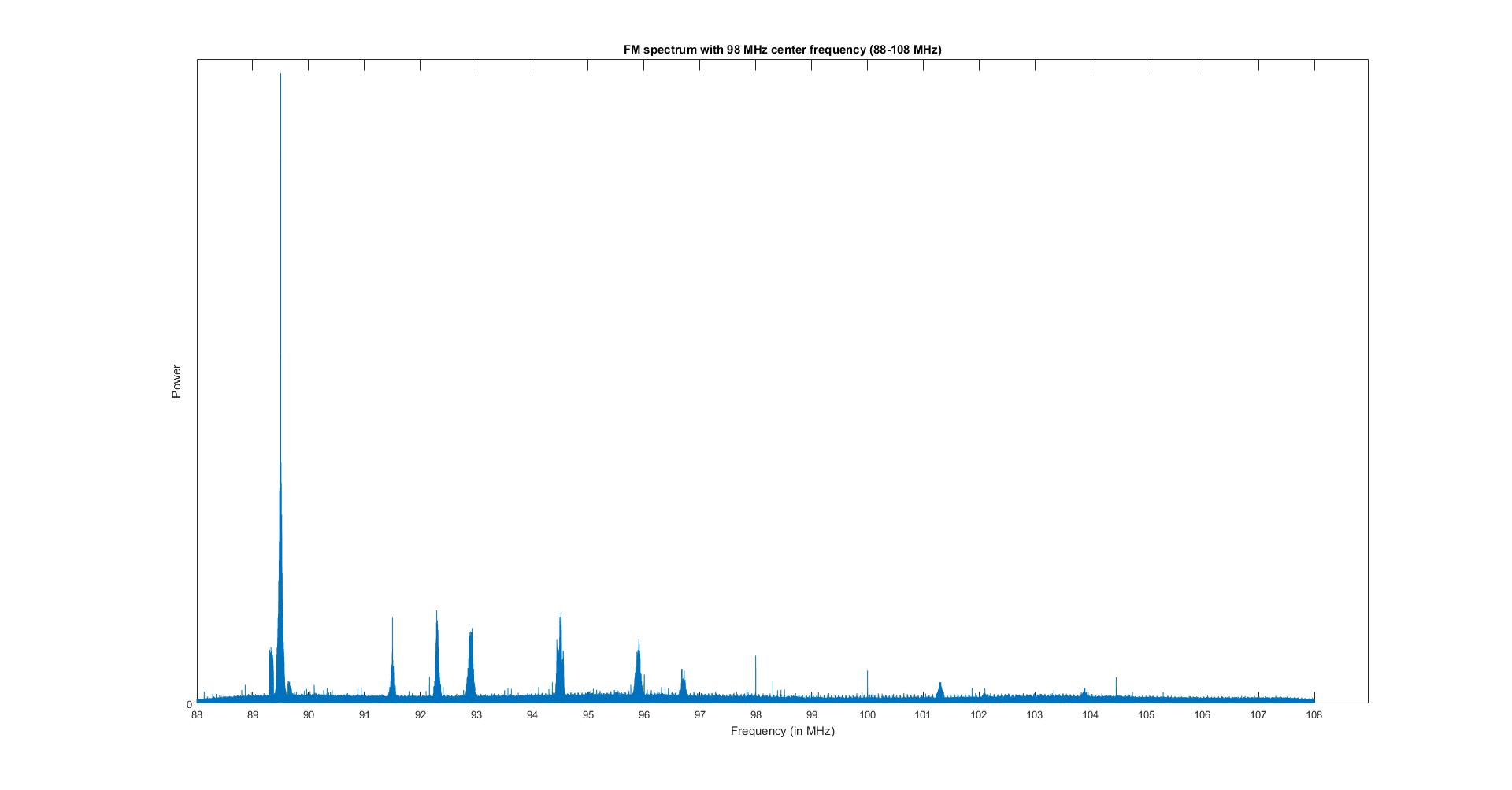
For example, consider the DTFT shown below. The frequency axis has been scaled and shifted to represent the frequency band from whence this signal was taken, but the amplitude values are DTFT values. Note that the spectrum is not symmetric. Therefore, the time domain signal must be complex valued. (The figure below shows the spectral band from 88 to 108 MHz. In the United States, this band is allocated for FM radio broadcasting. It is evident from the picture which stations are broadcasting.)