DTFT Multiplication Property - Example

The multiplication property of the DTFT states that multiplication in the time domain corresponds to periodic convolution in the frequency domain.

This property has several different names depending on the use or application. When one of the time-domain signals is a sinusoid, this property is called the modulation property of the DTFT because mixing/multiplication by a sinusoid is known as modulation. When one of the time-domain signals is a window (shaped finite length) function, this property is called the windowing property.

Windowing a sinusoidal signal

The figure below shows three signals:

1. An everlasting sinusoidal signal $x[n]$ with frequency $f_c=0.15$ cycles/sample,
2. a rectangular window $w[n]$ with length 11, and
3. the product $y[n] = x[n] w[n]$.

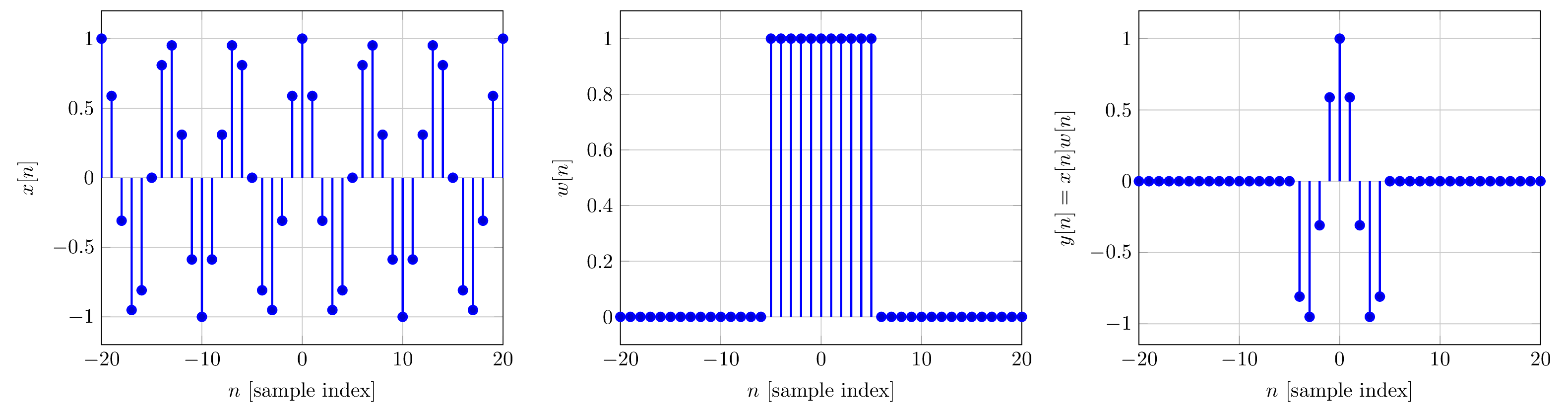
The action of multiplication by $w[n]$ reduces $x[n]$ to that part that can be seen through the window defined by $w[n]$.

The figure below shows the DTFTs of these three signals plotted over $-\frac{1}{2} \leq f \leq \frac{1}{2}$:

1. $X(f) = \frac{1}{2}\delta(f-f_c) + \frac{1}{2}\delta(f+f_c)$
2. $W(f) = \frac{\sin(\pi f (2N+1))}{\sin(\pi f)}$ for $N=11$
3. $Y(f) = X(f) \circledast W(f) = \frac{\sin(\pi [f-f_c] (2N+1))}{2\sin(\pi [f-f_c])} + \frac{\sin(\pi [f+f_c] (2N+1))}{2\sin(\pi [f+f_c])}$

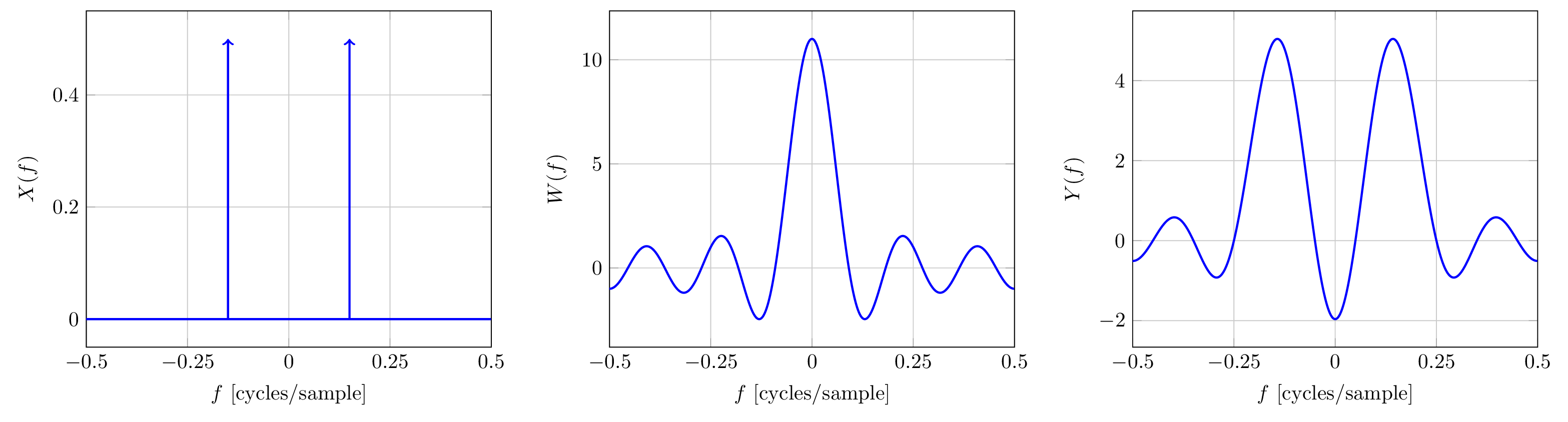
Notice that periodic convolution between $W(f)$ and the delta functions in $X(f)$, reproduces a copy of $W(f)$ at the frequency of the delta functions. The shifted copies $W(f-f_c)$ and $W(f+f_c)$ and their sum $Y(f)$ are shown in the figure below.

Consider the same example except that the length of the window is increased to 31 samples instead of 11 samples. The next two plots show the signals in time and frequency domains.

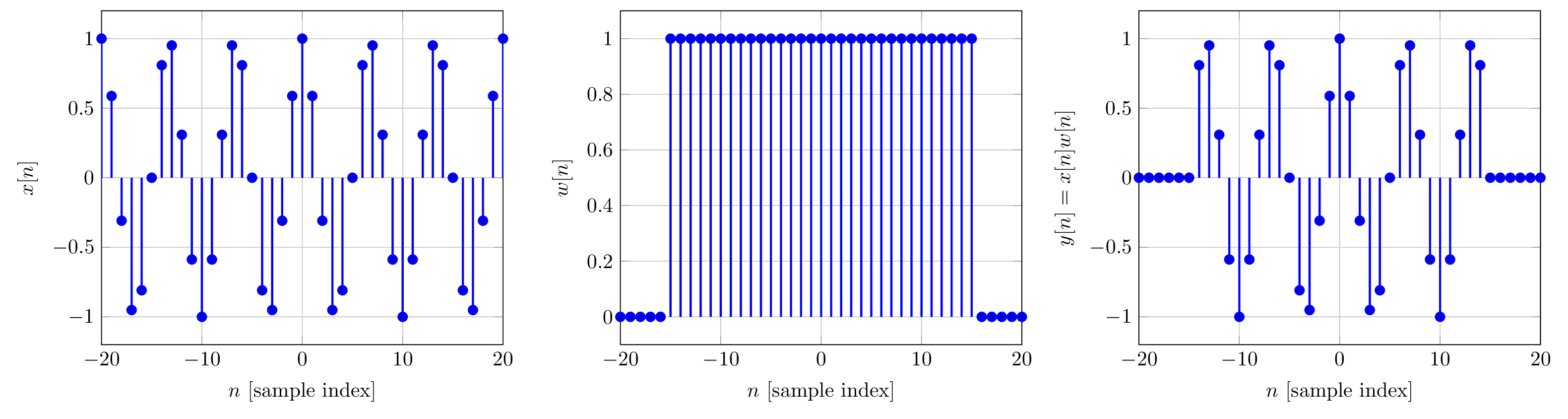
Notice that as the length of the time window $w[n]$ increases, the main lobe width of $W(f)$ decreases. The narrower main lobe width of longer time windows provides better spectral resolution.

Windowing an Ideal IIR filter impulse response

The figure below shows three signals:

1. The IIR impulse response $x[n]$ of an ideal low pass filter with cutoff frequency $f_c=0.15$ cycles/sample,
2. a rectangular window $w[n]$ with length 11, and
3. the product $y[n] = x[n] w[n]$.

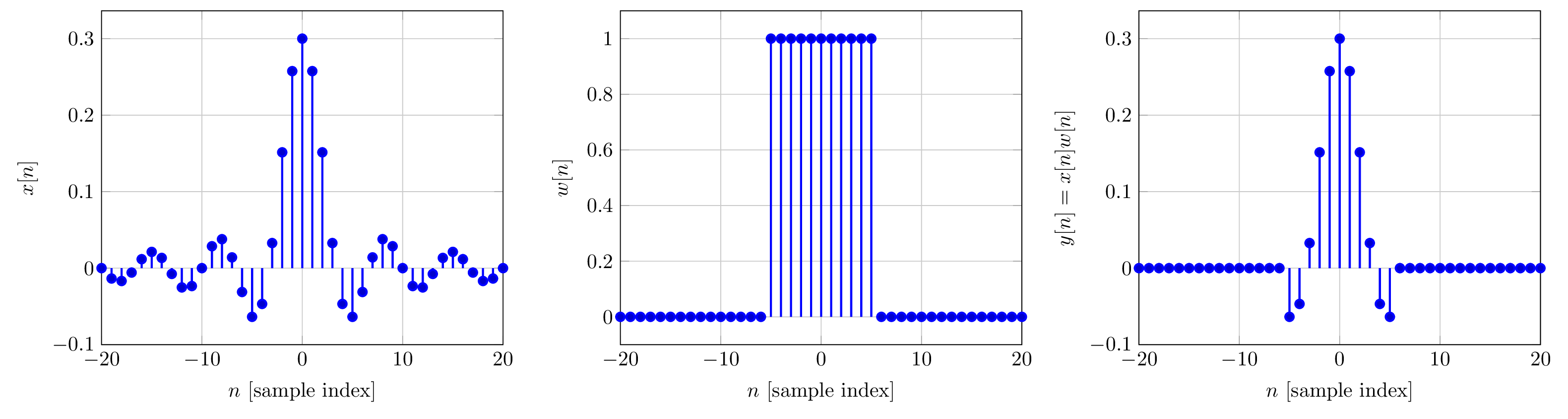
The action of multiplication by $w[n]$ reduces $x[n]$ to that part that can be seen through the window defined by $w[n]$. The advantage of $y[n]$ over $x[n]$ is that whereas $x[n]$ is unstable, noncausal and IIR, $y[n]$ is an finite length low pass filter that is stable and can be delayed by 5 samples to achieve causality. How good a low pass filter is $y[n]$? To answer that question, we have to look at the DTFT $Y(f)$.

The figure below shows the DTFTs of these three signals plotted over $-\frac{1}{2} \leq f \leq \frac{1}{2}$:

1. $X(f) = \begin{cases} 1, & |f|\leq f_c, \\ 0, & \text{otherwise}\end{cases}$
2. $W(f) = \frac{\sin(\pi f (2N+1))}{\sin(\pi f)}$ for $N=11$
3. $Y(f) = X(f) \circledast W(f)$

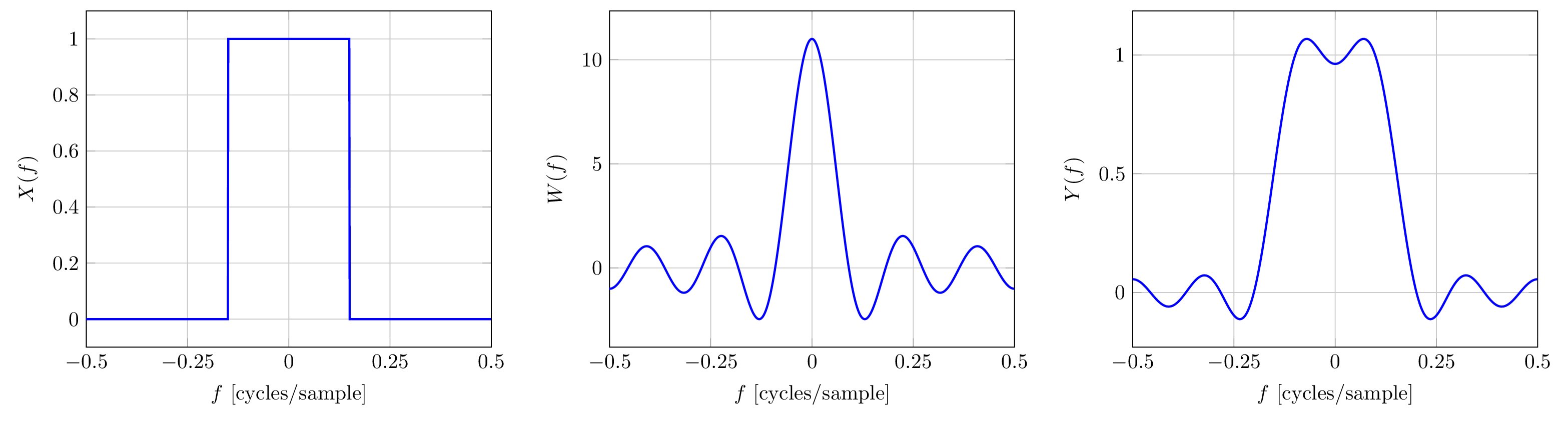
Notice that action of convolution with W(f) smears the crisp edges of $X(f)$. We can see that $Y(f)$ attenuates high frequencies and passes low frequencies. So it has low-pass filter characteristics. Another consequence of convolution with $W(f)$ is to produce a transition band between the pass and stop bands where $W(f)$ neither completely passes nor completely rejects frequencies in the input.

Consider the same example except that the length of the window is increased to 31 samples instead of 11 samples. The next two plots show the signals in time and frequency domains.

Notice that as the length of the time window $w[n]$ increases, the main lobe width of $W(f)$ decreases. The narrower main lobe width of longer time windows provides less smearing of the sharp edges of the ideal low pass filter leading to a narrower transition band.