DTFT Convolution Property - Example

The convolution property of the DTFT states that convolution in the time domain corresponds to multiplication in the frequency domain.

Consider the signal $x[n]$ whose spectrogram is shown below. (listen)

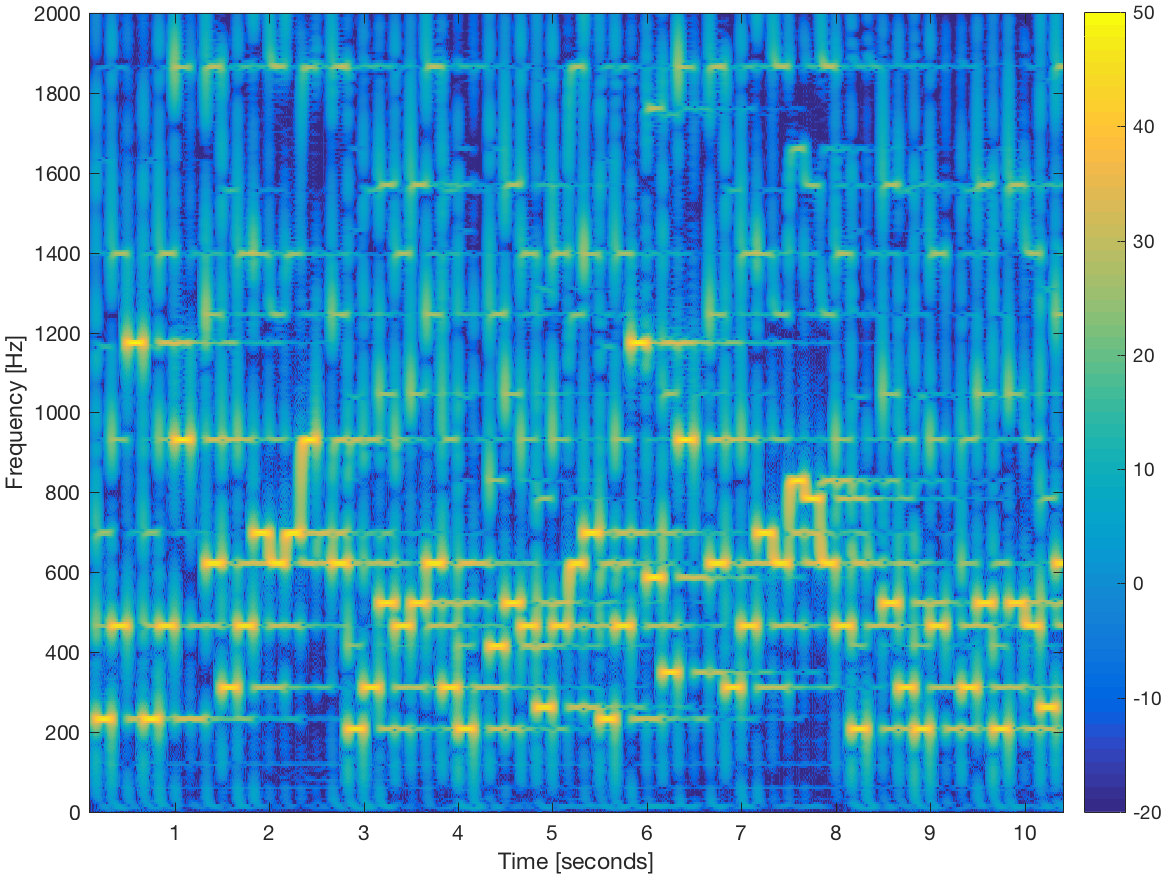
Note that only frequencies $0\leq f \leq 2000$ Hertz are shown.

This signal is input to the low-pass filter having magnitude frequency response shown below.

Note that multiplication by $H_\text{LPF}(f)$ in the frequency domain will suppress the output at high frequencies. The spectrogram of the output looks like this. (listen)

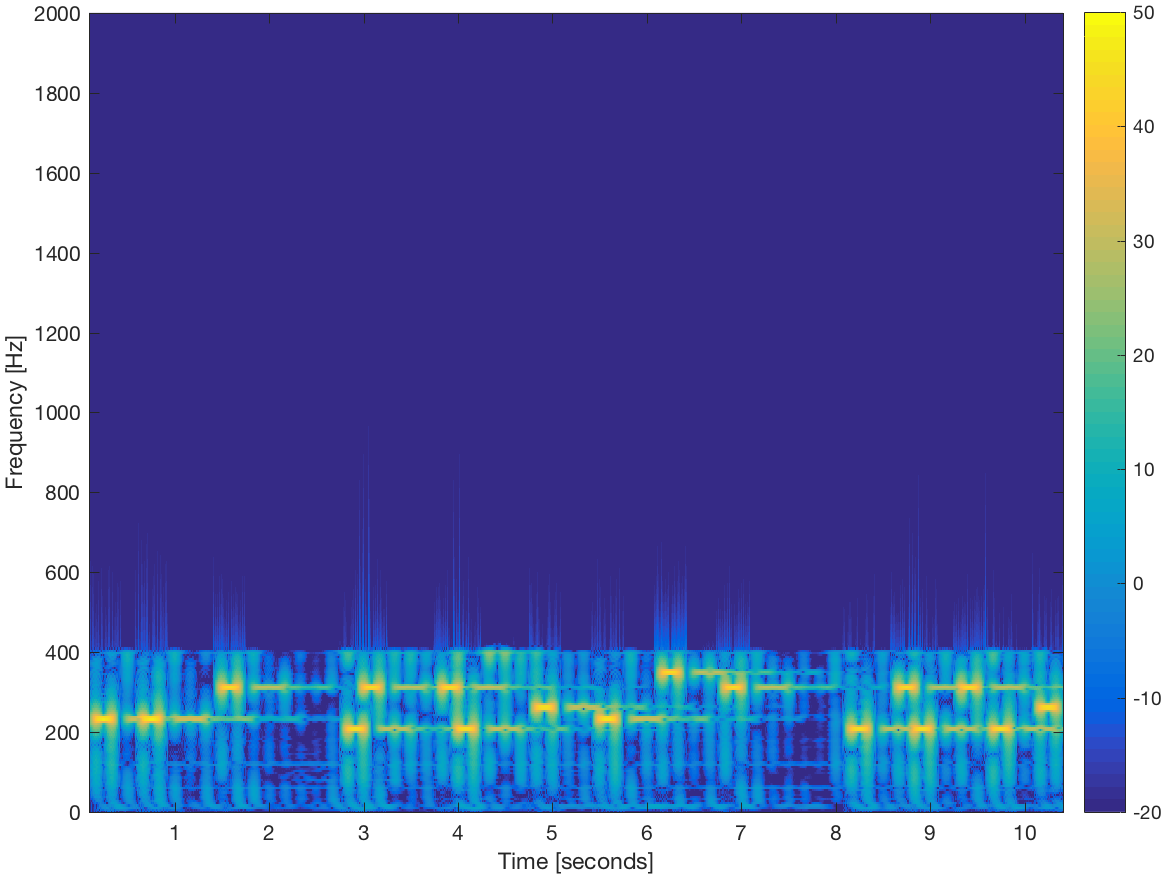
Notice that the filter output is the product of the input spectrum $X(f)$ with the filter response $H_\text{LPF}(f)$. As expected, the high frequencies are suppressed.

The signal is input to the high-pass filter having magnitude frequency response shown below.

Note that multiplication by $H_\text{HPF}(f)$ in the frequency domain will suppress the output at low frequencies. The spectrogram of the output looks like this. (listen)

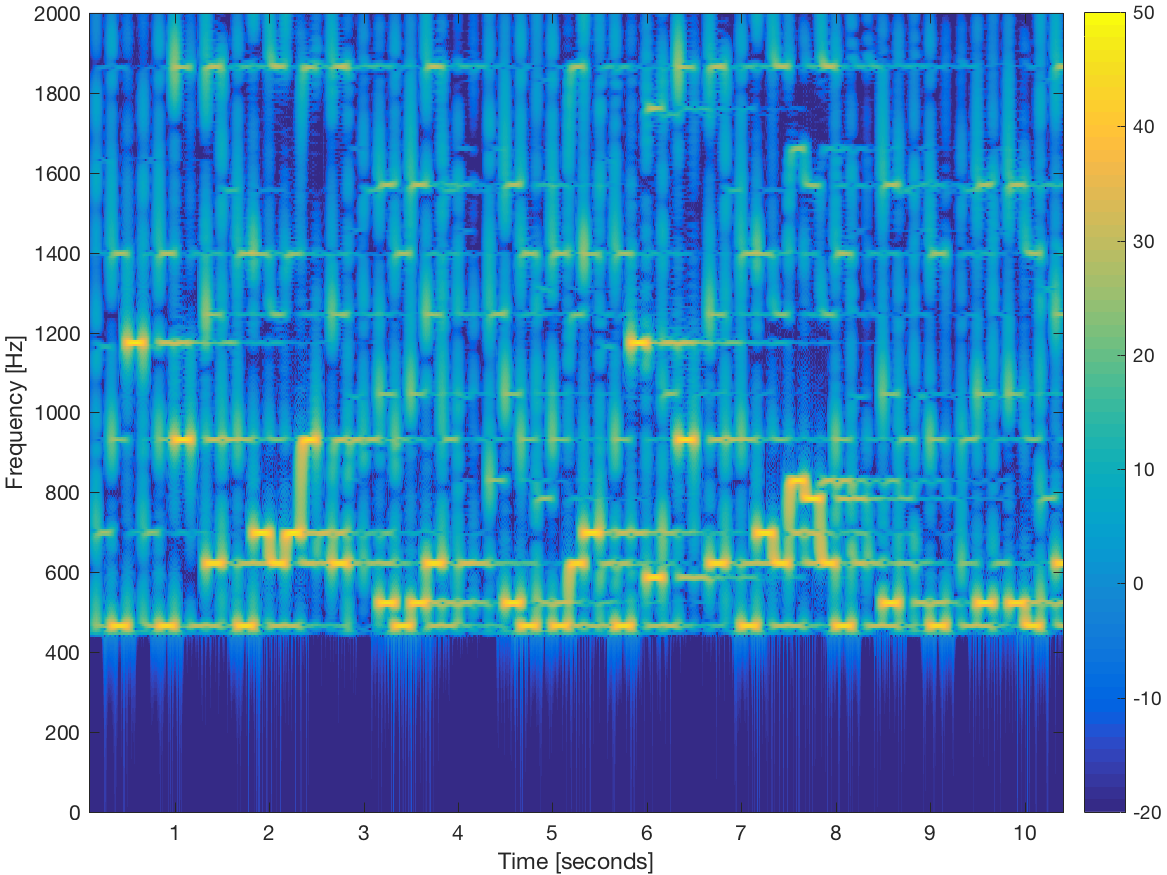
Notice that the filter output is the product of the input spectrum $X(f)$ with the filter response $H_\text{HPF}(f)$. As expected, the low frequencies are suppressed.

This example illustrates the convolution property of the DTFT.